[WITH CODE] Evaluation: Reengineer Machine Learning metrics
Is your strategy calibrated—or just lucky?
Table of contents:
Introduction.
Reimagining ML metrics for market dynamics.
The seven pillars of enhanced algorithmic trading.
Precision-recall trade-off or the profit-loss matrix.
ROC curves and the opportunity cost framework.
Matthews Correlation Coefficient as the balanced compass for alpha.
G-mean and balanced accuracy.
Cohen's Kappa for unmasking performance beyond pure chance.
Brier score and probabilistic calibration.
AUC-PR and imbalanced markets to find alpha in rare event.
Introduction
Today we operate at the intersection of two paradigms: the deterministic frameworks that form the backbone of quantitative finance and the adaptive pattern-recognition capabilities of machine learning. Traditional methodologies—refined through decades of rigorous statistical analysis, closed-form solutions, and stress-testing—provide interpretable models grounded in observable market relationships. Yet these approaches often falter when confronted with the non-stationary, reflexivity-driven nature of financial markets. The critical challenge lies in bridging the gap between the parsimony of analytical models and the often path-dependent dynamics of price.
Deploying machine learning in the markets introduces unique risks that demand rigorous scrutiny. Models trained on historical regimes frequently fail to adapt to structural breaks—black swan events, monetary policy shifts, or changes in market microstructure. Conventional performance metrics, such as accuracy scores or F1 measures, while useful for one approach may not be for another. Machine learning metrics are different from trading metrics and don't necessarily have the slightest correlation. But they can be very useful outside of machine learning with other approaches.
This divergence necessitates moving beyond classification metrics to focus on financial diagnostics: risk-adjusted returns, maximum drawdowns, regime-specific performance attribution, and robustness to stochastic volatility.
Reimagining ML metrics for market dynamics
Our path to this recalibration begins by recognizing the fundamental nature of the market: a place of profound asymmetry, where outcomes are rarely binary—success or failure—but rather exist on a spectrum of gains and losses. This is a world where the cost of being wrong often far outweighs the gains of being right, a truth that standard machine learning metrics optimized for symmetry largely ignore.
Trading systems, whether rules-based, analytical, or machine learning-based, must Trading systems, whether rules-based, analytical, or machine learning, must overcome all the hurdles that would break simpler algorithms designed for less adverse environments:
The underlying statistical properties of asset prices are not constant. Bull markets, bear markets, periods of high volatility, low volatility, crises, and calm phases each demand different trading logic. An algorithm tuned for one regime can be disastrously maladapted for another, rendering its historical "accuracy" moot.
Financial data is notoriously noisy. True predictive signals are often faint whispers lost in the roar of random price fluctuations, news headlines, and the collective irrationality of participants. The signal-to-noise ratio isn't a constant; it fluctuates, making consistent signal detection a monumental task.
Unlike classifying images or diagnosing medical conditions, the act of trading itself can influence the market. Large orders move prices. Successful strategies attract followers, diluting their effectiveness.
Profitable trading opportunities often exist within narrow temporal windows. A signal identified too late is useless. Evaluation metrics must implicitly or explicitly account for the timeliness of decisions.
The ultimate metric is risk-adjusted return, not just predictive accuracy. A model that predicts direction with 70% accuracy but loses more on its incorrect predictions than it gains on its correct ones is financially worthless. Our metrics must bridge this gap.
To master this environment, we must transcend the traditional interpretation of machine learning metrics. We must see them not just as indicators of statistical fit, but as proxies for financial outcomes.
You can check more about this here:
The seven pillars of enhanced algorithmic trading
Let's create a new foundation for a more effective evaluation framework by integrating machine learning metrics directly into the design and evaluation of algorithmic trading strategies. These seven pillars represent a technical synthesis that transforms abstract statistical measures into concrete tools.
Precision-recall trade-off or the profit-loss matrix
This is a zero-sum game and the cost of being wrong is often asymmetrical to the reward of being right. Standard precision and recall metrics, while useful, must be viewed through this lens of financial consequence. For a trading algorithm predicting a buy signal:
True positive: A predicted buy signal that results in a profitable trade. This is a successful capture of an opportunity.
False positive: A predicted buy signal that results in a losing trade. This is a direct capital loss.
True negative: No buy signal is predicted, and the market doesn't offer a profitable opportunity (or would result in a loss/flat trade). This is correctly avoiding a bad situation.
False negative: No buy signal is predicted, but the market did offer a profitable opportunity that was missed. This is an opportunity cost, a forgone gain.
Precision, defined as TP/(TP+FP), becomes the measure of the quality of our buy signals—what percentage of our predicted buys actually made money. Recall, TP/(TP+FN), measures the completeness—what percentage of available profitable opportunities did our system actually identify and attempt to capture?
Let’s code this to see an example:
import numpy as np
import pandas as pd
# Sample confusion matrix derived from trade outcomes
# Assuming a binary classification: Predict 1 for Buy, Actual 1 for Market Up (leading to profit)
# Predict 1 for Buy, Actual 0 for Market Down/Flat (leading to loss or flat)
# Predict 0 for No Trade, Actual 1 for Market Up (missed opportunity)
# Predict 0 for No Trade, Actual 0 for Market Down/Flat (correctly avoided)
conf_matrix_trades = {
'true_positives': 150, # Trades where system bought AND market went up (profitable)
'false_positives': 100, # Trades where system bought AND market went down/flat (losing)
'true_negatives': 200, # Periods where system didn't buy AND market went down/flat (avoided loss)
'false_negatives': 50 # Periods where system didn't buy AND market went up (missed profit)
}
# Calculate precision and recall based on trade outcomes
# Precision: Out of trades taken (TP+FP), how many were profitable (TP)?
precision = conf_matrix_trades['true_positives'] / (conf_matrix_trades['true_positives'] + conf_matrix_trades['false_positives'])
# Recall: Out of all profitable opportunities (TP+FN), how many did the system take (TP)?
recall = conf_matrix_trades['true_positives'] / (conf_matrix_trades['true_positives'] + conf_matrix_trades['false_negatives'])
print(f"Trade-based Precision: {precision:.4f}")
print(f"Trade-based Recall: {recall:.4f}")
# Now, introduce the financial asymmetry: average profit vs. average loss per trade
avg_profit_per_trade = 0.8 # Average percentage gain per successful trade
avg_loss_per_trade = -1.2 # Average percentage loss per unsuccessful trade
# Calculate the expected profit (or loss) across all trades taken
expected_profit_per_trade_instance = (conf_matrix_trades['true_positives'] * avg_profit_per_trade +
conf_matrix_trades['false_positives'] * avg_loss_per_trade)
print(f"Expected Profit from executed trades: {expected_profit_per_trade_instance:.2f}%")
# Profitability depends on the balance
# Total Profit = (TP * Avg_Profit) + (FP * Avg_Loss)
# For profitability, Total Profit > 0
# TP * Avg_Profit > - (FP * Avg_Loss)
# TP * Avg_Profit > FP * |Avg_Loss|
# Divide by (TP + FP):
# (TP / (TP + FP)) * Avg_Profit > (FP / (TP + FP)) * |Avg_Loss|
# Precision * Avg_Profit > (1 - Precision) * |Avg_Loss|
# Precision * Avg_Profit + Precision * |Avg_Loss| > |Avg_Loss|
# Precision * (Avg_Profit + |Avg_Loss|) > |Avg_Loss|
# Precision > |Avg_Loss| / (Avg_Profit + |Avg_Loss|)
# This gives us the critical "profitability threshold" for precision
profitability_threshold_precision = abs(avg_loss_per_trade) / (avg_profit_per_trade + abs(avg_loss_per_trade))
print(f"Minimum Precision required for profitability: {profitability_threshold_precision:.4f}")
# Compare actual precision to the threshold
if precision > profitability_threshold_precision:
print("Actual precision is above the profitability threshold.")
else:
print("Actual precision is below or at the profitability threshold. Likely unprofitable given these average outcomes.")Let’s visualize it:
The mathematics here is brutal and clear:
For the system to be profitable on the trades it takes, this value must be positive. This translates directly to a critical precision threshold:
Below this line in the sand, no amount of recall can save the strategy; it's simply picking too many losers relative to its winners, weighted by the average outcome magnitudes. This is the first perspective shift—moving from statistical correctness to the economic viability demanded by the market.
ROC curves and the opportunity cost framework
The ROC curve, typically a visualization of the tradeoff between True Positive Rate—Sensitivity/Recall—and False Positive Rate—Specificity—transforms into a mapping of financial opportunity costs. The standard curve helps choose a classification threshold by visualizing how TPR and FPR change. In trading, each point on this curve doesn't just represent a statistical balance; it represents a potential operational point for our algorithm, where a specific level of willingness to trigger trades—higher TPR—comes at the cost of accepting more bad signals—higher FPR.
Instead of optimizing for the point closest to [0,1] or maximizing the Area Under the Curve—known as AUC-ROC—which implicitly weights False Positives and False Negatives symmetrically, we must optimize for maximum financial outcome.
The mathematical relationship between the ROC curve and profitability at a given threshold t (which determines the specific TPR(t) and FPR(t)) is:
Assuming here that we only trade when the model gives a positive signal, and the 'negative' class corresponds to no trade or a short trade treated symmetrically but for simplicity focusing on long signals.
The optimal trading threshold t* is therefore:
This point rarely coincides with the traditional ML optimum. You can use the next snippet for that:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve
# Example data for True Labels (1 = Positive, 0 = Negative) and predicted scores
y_true = np.array([1, 0, 1, 1, 0, 0, 1, 1, 0, 0])
y_scores = np.array([0.9, 0.1, 0.8, 0.85, 0.2, 0.3, 0.95, 0.7, 0.05, 0.2])
# Define average profit and loss for trading
avg_profit = 10 # Example average profit for a true positive
avg_loss = 5 # Example average loss for a false positive
# Calculate ROC curve data
fpr, tpr, thresholds = roc_curve(y_true, y_scores)
# Calculate profit function for each threshold
profit = tpr * avg_profit - fpr * avg_loss
# Find optimal threshold based on maximizing profit
optimal_threshold_index = np.argmax(profit)
optimal_threshold = thresholds[optimal_threshold_index]
optimal_profit = profit[optimal_threshold_index]Let’s visualize this:
This perspective shift reveals that a trading system needs a different kind of calibration than a standard classifier. We are not just identifying a boundary; we are identifying a threshold that maximizes the expected return, directly incorporating the asymmetric costs of incorrect decisions.
Matthews Correlation Coefficient as the balanced compass for alpha
It is a metric often overlooked in simpler analyses, but it holds particular power for algorithmic trading because it provides a single, balanced measure of classification quality that accounts for all four quadrants of the confusion matrix (TP, TN, FP, FN), even with severe class imbalance.
MCC is defined as:
It ranges from -1—perfect inverse prediction—to +1—perfect prediction—with 0 indicating performance no better than random guessing. Why is this key for trading?
Profitable trading opportunities—the positive class—are often rare events in the market. A simple accuracy metric or even F1 score can be misleading in such imbalanced scenarios. MCC provides a more honest view of the algorithm's performance across both positive and negative cases, giving a better sense of its overall predictive skill, not just its ability to guess the majority class.
An MCC close to -1 is typically bad in standard classification. In trading, it could be gold. A consistent negative correlation might indicate a model that is perfectly wrong – and can be profitably traded in reverse. MCC helps explicitly identify such inverse edge.
A high MCC suggests the model's predictions are genuinely correlated with market movement outcomes in a way that considers both hits and misses on both sides. This provides a stronger indication of a real edge than metrics easily skewed by imbalance.
While the standard MCC is powerful, we can push it further. This snippet introduces a return-adjusted MCC concept:
def calculate_trading_mcc(predictions, actual_outcomes, trade_returns_for_positives, trade_returns_for_negatives):
"""
Calculate a Matthews Correlation Coefficient for trading, considering
actual trade outcomes and potentially return magnitudes.
Parameters:
predictions - binary predictions (e.g., 1 for Buy, 0 for No Trade)
actual_outcomes - binary actual results (e.g., 1 for Market Up/Profitable, 0 for Market Down/Flat/Loss)
This should align with what constitutes TP/FN for the prediction=1 case.
trade_returns_for_positives - List of returns for instances where actual_outcome is 1
trade_returns_for_negatives - List of returns for instances where actual_outcome is 0
"""
if len(predictions) != len(actual_outcomes):
raise ValueError("Predictions and actual outcomes must have the same length")
tp = sum((p == 1) and (a == 1) for p, a in zip(predictions, actual_outcomes))
fp = sum((p == 1) and (a == 0) for p, a in zip(predictions, actual_outcomes))
tn = sum((p == 0) and (a == 0) for p, a in zip(predictions, actual_outcomes))
fn = sum((p == 0) and (a == 1) for p, a in zip(predictions, actual_outcomes))
# Handle cases where denominator is zero
denominator = np.sqrt((tp + fp) * (tp + fn) * (tn + fp) * (tn + fn))
mcc_standard = (tp * tn - fp * fn) / denominator if denominator != 0 else 0.0
# A more complex return-weighted MCC could involve adjusting TP, FP counts
# by the magnitude of returns, or using a weighted sum in the numerator.
# The example in the prompt shows one interpretation - weighting the standard MCC
# by the ratio of summed TP returns to summed FP returns. Let's refine that concept.
# This is a non-standard MCC variant for illustration.
# Calculate sums of returns for trades taken based on prediction=1
total_tp_returns = sum(ret for p, a, ret in zip(predictions, actual_outcomes, trade_returns_for_positives + [0]*len(trade_returns_for_negatives)) if p == 1 and a == 1) # Simplified sum
total_fp_returns = sum(ret for p, a, ret in zip(predictions, actual_outcomes, [0]*len(trade_returns_for_positives) + trade_returns_for_negatives) if p == 1 and a == 0) # Simplified sum
# Avoid division by zero or zero loss scenario for weighting
if total_tp_returns > 0 and abs(total_fp_returns) > 0:
# Weight MCC by the profit/loss ratio from trades taken
mcc_return_weighted = mcc_standard * (total_tp_returns / abs(total_fp_returns))
else:
mcc_return_weighted = mcc_standard # No trades or no losses to weight by
return {
"mcc_standard": mcc_standard,
"mcc_return_weighted": mcc_return_weighted # A custom, non-standard variant
}
# Example data
predictions = [1, 1, 0, 1, 0] # Predicted buy/no trade actions
actual_outcomes = [1, 0, 1, 1, 0] # Actual market outcomes (1 = profitable, 0 = loss/flat)
trade_returns_for_positives = [0.05, 0.07, 0.03] # Returns from the trades where the market was profitable
trade_returns_for_negatives = [-0.02, -0.05] # Returns from the trades where the market was non-profitable
# Call the function
result = calculate_trading_mcc(predictions, actual_outcomes, trade_returns_for_positives, trade_returns_for_negatives)
# Output the results
print(f"Standard MCC: {result['mcc_standard']}")
print(f"Return-weighted MCC: {result['mcc_return_weighted']}")The power of MCC lies in its ability to summarize the confusion matrix into a single score that isn't distorted by class imbalance. A high MCC for a trading signal indicates a strong, balanced relationship between the signal and actual market outcomes, suggesting genuine predictive power beyond random chance or simply following a trend.
G-mean and balanced accuracy
Markets never offer a single, consistent environment. They cycle through distinct regimes—periods of trending, ranging, high volatility, low volatility, crisis, recovery. An algorithm might be a star performer in one regime and a liability in another. Metrics are needed to evaluate performance across these different market states. G-mean and balanced accuracy provide this perspective.
G-mean: The geometric mean of sensitivity—true positive rate—and specificity—true negative rate:
\(\text{G-Mean} = \sqrt{\text{TPR} \times \text{TNR}} = \sqrt{\frac{TP}{TP + FN} \times \frac{TN}{TN + FP}}\)Balanced accuracy: The arithmetic mean of sensitivity and specificity:
\(\text{Balanced Accuracy} = \frac{\text{TPR} + \text{TNR}}{2} = \frac{1}{2}\left(\frac{TP}{TP + FN} + \frac{TN}{TN + FP}\right)\)
These metrics are balanced because they average performance on the positive class—measured by TPR—and the negative class—measured by TNR. Why is this crucial for trading regimes?
Imagine an algorithm designed to identify bullish opportunities—positive class. In a strong bull market—regime A—it might have high TPR—identifying many opportunities—but low TNR—falsely identifying 'no opportunity' in many up periods. In a bear market—regime B—it might have low TPR—few opportunities to find—but high TNR—correctly identifying 'no opportunity' in many down periods. Standard accuracy could look decent in both if the majority class dominates. However, the G-mean or balanced accuracy, by averaging performance on both finding opportunities and correctly identifying non-opportunities, would reveal if the system is fundamentally imbalanced in its predictive power across states.
By calculating G-mean and balanced accuracy specifically for data segments corresponding to different identified market regimes, we gain invaluable insight:
A high G-mean/balanced accuracy across multiple regimes suggests an all-weather algorithm with robust performance characteristics.
A high score in one regime but low in others clearly flags a regime-dependent strategy.
import math
from typing import Sequence, Union
def _confusion_matrix_elements(y_true: Sequence[Union[int, bool]], y_pred: Sequence[Union[int, bool]]):
"""
Compute basic confusion matrix elements: TP, TN, FP, FN.
Assumes positive class is encoded as 1 or True, negative as 0 or False.
"""
tp = sum(1 for yt, yp in zip(y_true, y_pred) if yt and yp)
tn = sum(1 for yt, yp in zip(y_true, y_pred) if not yt and not yp)
fp = sum(1 for yt, yp in zip(y_true, y_pred) if not yt and yp)
fn = sum(1 for yt, yp in zip(y_true, y_pred) if yt and not yp)
return tp, tn, fp, fn
def gmean_score(y_true: Sequence[Union[int, bool]], y_pred: Sequence[Union[int, bool]]) -> float:
"""
Calculate the G-Mean: the geometric mean of sensitivity (TPR) and specificity (TNR).
G-Mean = sqrt(TPR * TNR)
where
TPR = TP / (TP + FN)
TNR = TN / (TN + FP)
"""
tp, tn, fp, fn = _confusion_matrix_elements(y_true, y_pred)
tpr = tp / (tp + fn) if (tp + fn) > 0 else 0.0
tnr = tn / (tn + fp) if (tn + fp) > 0 else 0.0
return math.sqrt(tpr * tnr)
def balanced_accuracy(y_true: Sequence[Union[int, bool]], y_pred: Sequence[Union[int, bool]]) -> float:
"""
Calculate the Balanced Accuracy: the arithmetic mean of sensitivity (TPR) and specificity (TNR).
Balanced Accuracy = (TPR + TNR) / 2
"""
tp, tn, fp, fn = _confusion_matrix_elements(y_true, y_pred)
tpr = tp / (tp + fn) if (tp + fn) > 0 else 0.0
tnr = tn / (tn + fp) if (tn + fp) > 0 else 0.0
return 0.5 * (tpr + tnr)
# Sample true and predicted labels (1 for opportunity, 0 for no opportunity)
y_true = [1, 0, 1, 1, 0, 0, 1, 0]
y_pred = [1, 0, 1, 0, 0, 1, 1, 0]
# Metrics
print("G-ean:", gmean_score(y_true, y_pred))
print("Balanced accuracy:", balanced_accuracy(y_true, y_pred))Let’s visualize it:
It rewards classifiers that perform well on both classes and penalizes those that excel on one at the expense of the other. This makes G-mean particularly valuable in imbalanced settings—like different market regimes—where a model must be all-weather, detecting opportunities without over-reacting to non-opportunities.
Cohen's Kappa for unmasking performance beyond pure chance
In environments defined by noise and potential spurious correlations, distinguishing genuine skill from random luck is paramount. Cohen's Kappa statistic provides a formal way to do this. It measures the agreement between two raters—in our case, the algorithm's prediction and the actual market outcome—while accounting for the agreement that would be expected by random chance.
The formula for Cohen's Kappa is:
Where Po is the observed accuracy—proportion of instances where prediction matches outcome—and Pe is the expected accuracy by random chance.
For algorithmic trading, calculating Pe is key. It's not just 50% for a binary outcome. It depends on the marginal probabilities of the predictor and the actual outcome. In trading, the actual outcome probability might reflect the underlying market trend. If the market went up 60% of the time in our test period, a naive always predict up strategy would have 60% accuracy. Cohen's Kappa adjusts for this inherent bias in the data's outcome distribution.
This snippet illustrates a market-adjusted Kappa:
def calculate_trading_kappa(predictions, actual_movements, market_trend_probability=0.5):
"""
Calculate Cohen's Kappa, adjusting for the expected agreement based
on market trend probability.
Parameters:
predictions - binary predictions (1 for Buy/Up, 0 for No Trade/Down)
actual_movements - actual binary market outcomes (1 for Up, 0 for Down/Flat)
market_trend_probability - historical probability of market 'Up' movement
in the evaluation period.
"""
if len(predictions) != len(actual_movements):
raise ValueError("Predictions and actual movements must have the same length")
total_instances = len(predictions)
if total_instances == 0:
return {"observed_accuracy": 0.0, "expected_accuracy": 0.0, "kappa": 0.0}
# Calculate observed accuracy (Po)
correct_predictions = sum(p == a for p, a in zip(predictions, actual_movements))
observed_accuracy = correct_predictions / total_instances
# Calculate expected accuracy by chance (Pe)
# Pe = P(Predict 1 and Actual 1) + P(Predict 0 and Actual 0)
# P(Predict 1) = (Number of 1 predictions) / Total Instances
# P(Actual 1) = market_trend_probability
# P(Predict 0) = (Number of 0 predictions) / Total Instances
# P(Actual 0) = 1 - market_trend_probability
prob_predict_1 = sum(p == 1 for p in predictions) / total_instances
prob_predict_0 = 1 - prob_predict_1
# Assuming independence for chance calculation
pe_predict_1_actual_1 = prob_predict_1 * market_trend_probability
pe_predict_0_actual_0 = prob_predict_0 * (1 - market_trend_probability)
expected_accuracy = pe_predict_1_actual_1 + pe_predict_0_actual_0
# Calculate Cohen's Kappa
# Prevent division by zero if expected_accuracy is 1 (perfect chance agreement, unlikely)
kappa = (observed_accuracy - expected_accuracy) / (1 - expected_accuracy) if expected_accuracy < 1 else 0.0
return {
"observed_accuracy": observed_accuracy,
"expected_accuracy": expected_accuracy,
"kappa": kappa
}
# Example Usage:
Assuming predictions = [1, 0, 1, 1, 0], actual_movements = [1, 0, 0, 1, 1]
# Market had 3/5 = 0.6 probability of going up in this period.
example_predictions = [1, 0, 1, 1, 0]
example_actuals = [1, 0, 0, 1, 1]
example_market_trend = 3/5 # or 0.6
kappa_results = calculate_trading_kappa(example_predictions, example_actuals, example_market_trend)
print(kappa_results)A Kappa value significantly greater than zero suggests that the algorithm's agreement with actual market movements is better than would be expected if the algorithm's predictions and the market's movements were independent random events with the same marginal probabilities.
In essence, a positive Kappa provides mathematical evidence that the algorithm possesses some level of skill or edge beyond merely riding the prevailing market trend or making random calls. It helps separate strategies that got lucky in a trending market from those that actually identified opportunities.
Brier score and probabilistic calibration—the granular edge in risk
Many classification metrics force us into a binary yes/no decision. Trading, however, is fundamentally probabilistic and requires nuance for effective risk management. A model that outputs a probability estimate—e.g., 70% chance the market goes up—is far more valuable than one that simply says buy. The Brier score is a metric specifically designed to evaluate the accuracy of these probability predictions.
The Brier score measures the mean squared difference between the predicted probability and the actual outcome—where the outcome is 1 for true, 0 for false:
Where yi is the actual outcome—1 or 0—and pi is the predicted probability of the outcome being 1. A lower Brier Score indicates better-calibrated probabilities.
Why is probabilistic calibration, evaluated by the Brier score?
How much capital to allocate to a given trade? A higher predicted probability/confidence should ideally translate into a larger position size—within risk limits)—while lower confidence suggests a smaller or zero position. Well-calibrated probabilities are essential for making these decisions optimally.
Instead of a simple stop-loss on every trade, probabilistic estimates allow for dynamic risk allocation. Trades with lower predicted probabilities might warrant tighter stops or smaller sizes.
The market isn't just up or down; the likelihood of moving up by a certain amount matters. Probabilistic models and their calibration capture this nuance.
The next snippet shows how a Brier-score-informed approach can influence position sizing:
import numpy as np
def calibration_based_position_sizing(prediction_probabilities, historical_brier_scores, portfolio_value,
base_position_pct=0.01, max_position_pct=0.10):
"""
Calculate position sizes based on prediction probabilities and
historical model calibration quality (using Brier Score).
Parameters:
prediction_probabilities - A single predicted probability (0 to 1) for a positive outcome.
historical_brier_scores - List of recent Brier scores for the model (lower is better).
portfolio_value - Current total portfolio value.
base_position_pct - Base position size as a fraction of portfolio value for high confidence/calibration.
max_position_pct - Maximum allowed position size as a fraction of portfolio value.
"""
if portfolio_value <= 0:
return 0.0 # Cannot size position with zero or negative value
# Calculate recent calibration quality based on historical Brier scores
# We want higher quality for lower Brier scores.
# Let's inverse and scale Brier scores (e.g., scale Brier from 0 to 0.25)
# A Brier score of 0 is perfect, 0.25 is like 50/50 random guessing on average.
# Calibration Quality = 1 - (recent_brier / max_expected_brier) -> scaled 0 to 1
# A common reference point is 0.25 for a random classifier on balanced data.
# Let's use a simple inversion and normalization based on a conceptual max Brier of ~0.25-0.30 for a binary case.
# Adjusting scaling: Lower Brier means better calibration quality.
# calibration_quality near 1 for Brier near 0, near 0 for Brier near 0.25+
recent_brier = np.mean(historical_brier_scores[-50:]) if historical_brier_scores else 0.25 # Use last 50, default if empty
# Simple inverse scaling: 1 - (brier / MaxExpectedBrier). If MaxExpectedBrier is 0.25, quality = 1 - brier/0.25
# Clip brier to avoid negative quality or quality > 1
recent_brier_clipped = np.clip(recent_brier, 0, 0.25)
calibration_quality = 1 - (recent_brier_clipped / 0.25) # Scales Brier [0, 0.25] to Quality [1, 0]
# Calculate prediction confidence from the probability
# Confidence is how far the probability is from 0.5 (no edge)
# Confidence ranges from 0 (prob 0.5) to 1 (prob 0 or 1)
prediction_confidence = 2 * abs(prediction_probabilities - 0.5) # Scales |prob-0.5| [0, 0.5] to Confidence [0, 1]
# Determine trade direction based on probability threshold (e.g., 0.5)
direction = 1 if prediction_probabilities > 0.5 else (-1 if prediction_probabilities < 0.5 else 0) # 0 for neutral
# Calculate base position size scaled by confidence and calibration quality
# Only consider trading if there's a directional signal (probability not 0.5)
if direction != 0:
# Position size scales with both prediction confidence AND calibration quality
# More confidence AND better calibration -> larger size
# Scale base size up to max size based on combined score
scaled_position_pct = base_position_pct + (max_position_pct - base_position_pct) * (calibration_quality * prediction_confidence)
position_size_pct = direction * scaled_position_pct
else:
position_size_pct = 0.0 # No position if no clear directional signal
# Enforce overall maximum position size percentage
position_size_pct = np.clip(position_size_pct, -max_position_pct, max_position_pct)
# Convert to absolute currency amount
position_value = position_size_pct * portfolio_value
return position_value
# Example Usage:
model_prob = 0.7 # Model predicts 70% chance of going up
recent_briers = [0.15, 0.12, 0.18, 0.14] # Recent Brier scores
current_portfolio_value = 100000
position = calibration_based_position_sizing(model_prob, recent_briers, current_portfolio_value)
print(f"Predicted probability: {model_prob}")
print(f"Recent Brier scores: {recent_briers}")
print(f"Calculated position size: ${position:.2f}")
model_prob_low_conf = 0.55 # Lower confidence
position_low_conf = calibration_based_position_sizing(model_prob_low_conf, recent_briers, current_portfolio_value)
print(f"\nPredicted probability (low confidence): {model_prob_low_conf}")
print(f"Recent Brier scores: {recent_briers}")
print(f"Calculated position size: ${position_low_conf:.2f}")
model_prob_poor_calibration = 0.7 # Same probability, but imagine poor calibration
recent_briers_poor = [0.23, 0.21, 0.24, 0.22] # Higher Brier scores (worse calibration)
position_poor_cal = calibration_based_position_sizing(model_prob, recent_briers_poor, current_portfolio_value)
print(f"\nPredicted probability: {model_prob}")
print(f"Recent Brier scores (poor calibration): {recent_briers_poor}")
print(f"Calculated position size: ${position_poor_cal:.2f}")By continuously monitoring the Brier score, the system can dynamically adjust the confidence placed in the model's probability estimates. Even a model with high accuracy but poor calibration would be penalized, leading to smaller position sizes until its calibration improves.
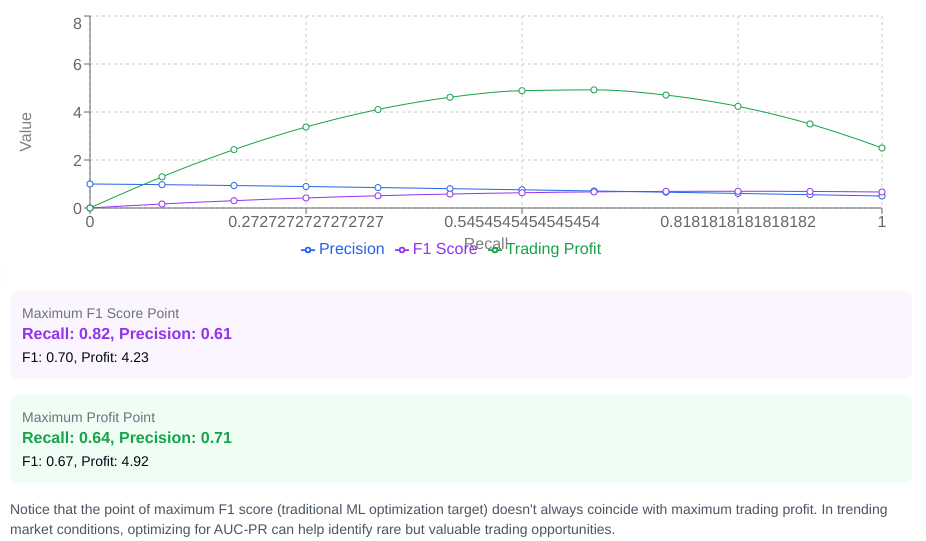
AUC-PR and imbalanced markets to find alpha in rare event
Financial markets are often characterized by extreme class imbalance. Truly significant profitable opportunities might occur only 10% or 20% of the time. In such scenarios, the traditional ROC curve and its AUC can be misleading because they include true negatives—correctly identifying non-opportunities—which are often the vast majority of instances and can inflate the AUC score even if the model is poor at identifying the rare positive cases.
The Area Under the Precision-Recall Curve is far more informative in these imbalanced conditions. The Precision-Recall curve give us the precision against. It focuses solely on the positive class and the types of errors directly related to trading outcomes—false positives causing losses, false negatives representing missed profits.
The distinction is vital:
ROC: TPR vs FPR—involves TP, FN, FP, TN.
PR: Precision vs Recall—involves TP, FP, FN.
When the positive class—profitable opportunities—is rare, the number of true negatives is large. This large TN count makes the false positive rate artificially low, potentially making a poor model look better on an ROC curve than it is at identifying actual opportunities. The PR curve, by ignoring TNs and focusing on the relationship between Precision and Recall, provides a more realistic view of performance on the minority, financially critical, class.
Mathematically, as we saw earlier, the expected profit depends directly on precision and recall, along with average profit/loss:
While the F1 score is the harmonic mean of Precision and Recall, maximizing F1 doesn't necessarily maximize profit when the ratio of average win to average loss is significantly different from 1:1. The PR curve allows us to visualize this tradeoff and select an operating point—a threshold—that balances precision and recall according to the financial payoff structure, not just their statistical harmony. AUC-PR provides a single aggregate measure of this capability in imbalanced markets.
from sklearn.metrics import average_precision_score
def calculate_auc_pr(predicted_probabilities, actual_outcomes):
"""
Returns the area under the precision–recall curve (AUC-PR).
If there are no positives in `actual_outcomes`, returns 0.0.
"""
if len(predicted_probabilities) != len(actual_outcomes):
raise ValueError("Length mismatch between predictions and actuals")
# average_precision_score handles empty or constant targets by returning 0.0
return average_precision_score(actual_outcomes, predicted_probabilities)
# Example
y_true = [0, 1, 0, 1, 0, 0, 1]
y_scores = [0.1, 0.9, 0.2, 0.8, 0.05, 0.4, 0.7]
auc_pr = calculate_auc_pr(y_scores, y_true)
print(f"AUC-PR = {auc_pr:.3f}")
Using AUC-PR helps quants identify models that are genuinely capable of finding profitable alpha in the sporadic moments it appears, rather than models that simply perform well on correctly identifying the frequent periods of no opportunity.
Epic work today, team! Tomorrow we push deeper into quant issues—where models battle noise and alpha hides in the shadows. Tonight, recalibrate your thinking, trust the math, and let every anomaly spark curiosity. Keep your edge sharp and your risk tighter. Stay fearless, stay quanty! 📊
PS: When you purchase a service on a trading platform which do you prefer?
This is an invitation-only access to our QUANT COMMUNITY, so we verify numbers to avoid spammers and scammers. Feel free to join or decline at any time. Tap the WhatsApp icon below to join
Appendix
Full script with metrics and some additioal help to choose:
The scritp with the metrics:
# Assuming helper functions like calculate_precision, calculate_recall, etc., are defined elsewhere
# based on the logic discussed in the 7 points.
# Assuming market_conditions is a dictionary containing info like {'trend_probability': 0.6, 'regimes': {'Trend': [indices], 'Range': [indices]}}
# Assuming predictions are binary trade signals (1/0) and actual_movements are binary outcomes (1/0)
# Assuming trade_returns is a list of returns for each instance (aligned with predictions/movements)
def calculate_precision(predictions, actual_movements):
tp = sum((p == 1) and (a == 1) for p, a in zip(predictions, actual_movements))
fp = sum((p == 1) and (a == 0) for p, a in zip(predictions, actual_movements))
return tp / (tp + fp) if (tp + fp) > 0 else 0.0
def calculate_recall(predictions, actual_movements):
tp = sum((p == 1) and (a == 1) for p, a in zip(predictions, actual_movements))
fn = sum((p == 0) and (a == 1) for p, a in zip(predictions, actual_movements))
return tp / (tp + fn) if (tp + fn) > 0 else 0.0
def calculate_balanced_accuracy(predictions, actual_movements):
tp = sum((p == 1) and (a == 1) for p, a in zip(predictions, actual_movements))
fn = sum((p == 0) and (a == 1) for p, a in zip(predictions, actual_movements))
tn = sum((p == 0) and (a == 0) for p, a in zip(predictions, actual_movements))
fp = sum((p == 1) and (a == 0) for p, a in zip(predictions, actual_movements))
tpr = tp / (tp + fn) if (tp + fn) > 0 else 0.0
tnr = tn / (tn + fp) if (tn + fp) > 0 else 0.0
return (tpr + tnr) / 2
def calculate_mcc(predictions, actual_movements):
tp = sum((p == 1) and (a == 1) for p, a in zip(predictions, actual_movements))
fp = sum((p == 1) and (a == 0) for p, a in zip(predictions, actual_movements))
tn = sum((p == 0) and (a == 0) for p, a in zip(predictions, actual_movements))
fn = sum((p == 0) and (a == 1) for p, a in zip(predictions, actual_movements))
denominator = np.sqrt((tp + fp) * (tp + fn) * (tn + fp) * (tn + fn))
return (tp * tn - fp * fn) / denominator if denominator != 0 else 0.0
# Need implementations for calculate_trading_kappa, calculate_g_mean, calculate_brier_score, calculate_auc_pr,
# calculate_profit_loss, calculate_sharpe_ratio, calculate_max_drawdown.
# (Assume these exist based on previous discussions or standard library functions where applicable)
def calculate_g_mean(predictions, actual_movements):
tp = sum((p == 1) and (a == 1) for p, a in zip(predictions, actual_movements))
fn = sum((p == 0) and (a == 1) for p, a in zip(predictions, actual_movements))
tn = sum((p == 0) and (a == 0) for p, a in zip(predictions, actual_movements))
fp = sum((p == 1) and (a == 0) for p, a in zip(predictions, actual_movements))
tpr = tp / (tp + fn) if (tp + fn) > 0 else 0.0
tnr = tn / (tn + fp) if (tn + fp) > 0 else 0.0
return np.sqrt(tpr * tnr)
# Dummy implementations for financial metrics for the example structure
def calculate_profit_loss(predictions, trade_returns):
# Assuming trade_returns contains the return for each instance, even if 0 for no trade
return sum(trade_returns)
def calculate_sharpe_ratio(predictions, trade_returns):
# Requires more context (risk-free rate, frequency) - simplified for structure
returns_series = pd.Series(trade_returns) # Use pandas for financial calcs
if returns_series.std() == 0 or len(returns_series) == 0:
return 0.0
# Simplified daily Sharpe (need actual annualization for real trading)
return returns_series.mean() / returns_series.std()
def calculate_max_drawdown(predictions, trade_returns):
# Requires equity curve - simplified for structure
equity_curve = (1 + pd.Series(trade_returns)).cumprod()
peak = equity_curve.expanding(min_periods=1).max()
drawdown = (equity_curve - peak) / peak
return abs(drawdown.min()) if len(drawdown) > 0 else 0.0
# Need actual Brier and AUC-PR functions (e.g., from sklearn.metrics)
from sklearn.metrics import brier_score_loss, auc, precision_recall_curve
def calculate_brier_score(predicted_probabilities, actual_outcomes):
# Assumes predicted_probabilities are available (0 to 1)
if len(predicted_probabilities) != len(actual_outcomes):
raise ValueError("Probabilities and actual outcomes must have the same length")
if not predicted_probabilities:
return 0.0
return brier_score_loss(actual_outcomes, predicted_probabilities) # sklearn handles arrays
def calculate_auc_pr(predicted_probabilities, actual_outcomes):
# Assumes predicted_probabilities are available (0 to 1)
if len(predicted_probabilities) != len(actual_outcomes):
raise ValueError("Probabilities and actual outcomes must have the same length")
if not predicted_probabilities:
return 0.0
precision, recall, _ = precision_recall_curve(actual_outcomes, predicted_probabilities)
return auc(recall, precision) # Area under the curve
# Dummy market_conditions structure
dummy_market_conditions = {
'trend_probability': 0.6, # Example: 60% historical chance of 'Up' movement
'regimes': {
'Overall': list(range(300)), # Indices for the whole period
'Trend_Regime_A': list(range(100)),
'Range_Regime_B': list(range(100, 200)),
'Volatile_Regime_C': list(range(200, 300))
}
}
# Dummy data for demonstration
# Assume 300 instances (e.g., daily periods)
np.random.seed(42)
dummy_predictions_binary = np.random.randint(0, 2, 300).tolist() # Example binary predictions
dummy_actual_outcomes_binary = np.random.randint(0, 2, 300).tolist() # Example binary outcomes
# Dummy returns - align with outcomes roughly
dummy_trade_returns = [ret if actual == 1 else -abs(ret) for actual, ret in zip(dummy_actual_outcomes_binary, np.random.rand(300)*0.01 + 0.005)] # Small random returns
# Dummy probabilities (needed for Brier, AUC-PR) - slightly correlated with outcomes
dummy_probabilities = [min(max(p + np.random.randn()*0.1, 0.05), 0.95) for p in dummy_actual_outcomes_binary]
def comprehensive_trading_evaluation(predictions_binary, predicted_probabilities, actual_outcomes_binary, trade_returns, market_conditions):
"""
A unified evaluation framework combining multiple ML metrics
with financial performance measures.
"""
# Ensure data lengths match
if not (len(predictions_binary) == len(predicted_probabilities) == len(actual_outcomes_binary) == len(trade_returns)):
raise ValueError("Input data lists must all have the same length.")
if not predictions_binary:
return "No data provided for evaluation."
# Calculate core statistical metrics
precision = calculate_precision(predictions_binary, actual_outcomes_binary)
recall = calculate_recall(predictions_binary, actual_outcomes_binary)
balanced_accuracy = calculate_balanced_accuracy(predictions_binary, actual_outcomes_binary)
mcc = calculate_mcc(predictions_binary, actual_outcomes_binary)
brier_score = calculate_brier_score(predicted_probabilities, actual_outcomes_binary)
auc_pr = calculate_auc_pr(predicted_probabilities, actual_outcomes_binary)
# Calculate market-adjusted metrics
# Need the overall market trend probability for Kappa
overall_trend_prob = market_conditions.get('trend_probability', 0.5) # Default to 0.5 if not provided
kappa_results = calculate_trading_kappa(predictions_binary, actual_outcomes_binary, overall_trend_prob)
market_adjusted_kappa = kappa_results['kappa']
# Calculate overall financial performance metrics
total_profit = calculate_profit_loss(predictions_binary, trade_returns) # Assumes trade_returns are P/L for each instance
sharpe_ratio = calculate_sharpe_ratio(predictions_binary, trade_returns)
max_drawdown = calculate_max_drawdown(predictions_binary, trade_returns)
# Calculate regime-specific performance
regime_performance = {}
if 'regimes' in market_conditions:
for regime, indices in market_conditions['regimes'].items():
if not indices: continue # Skip empty regimes
regime_predictions = [predictions_binary[i] for i in indices]
regime_outcomes = [actual_outcomes_binary[i] for i in indices]
regime_returns = [trade_returns[i] for i in indices]
regime_probabilities = [predicted_probabilities[i] for i in indices]
# Calculate metrics for the current regime
regime_g_mean = calculate_g_mean(regime_predictions, regime_outcomes)
regime_brier = calculate_brier_score(regime_probabilities, regime_outcomes)
regime_auc_pr = calculate_auc_pr(regime_probabilities, regime_outcomes)
# Financials for the regime
regime_profit = sum(regime_returns)
regime_sharpe = calculate_sharpe_ratio(regime_predictions, regime_returns) # Note: Sharpe needs meaningful returns sequence
regime_drawdown = calculate_max_drawdown(regime_predictions, regime_returns) # Note: Drawdown needs equity curve logic per regime
regime_performance[regime] = {
"g_mean": regime_g_mean,
"brier_score": regime_brier,
"auc_pr": regime_auc_pr,
"profit": regime_profit,
"sharpe": regime_sharpe,
"drawdown": regime_drawdown
}
# Construct the comprehensive evaluation report
evaluation_report = {
"statistical_metrics": {
"precision": precision,
"recall": recall,
"balanced_accuracy": balanced_accuracy,
"mcc": mcc,
"brier_score": brier_score,
"auc_pr": auc_pr,
"market_adjusted_kappa": market_adjusted_kappa
},
"financial_metrics": {
"total_profit": total_profit,
"sharpe_ratio": sharpe_ratio,
"max_drawdown": max_drawdown
},
"regime_performance": regime_performance
}
return evaluation_report
# Run the comprehensive evaluation with dummy data
comprehensive_results = comprehensive_trading_evaluation(
dummy_predictions_binary,
dummy_probabilities, # Pass probabilities for Brier/AUC-PR
dummy_actual_outcomes_binary,
dummy_trade_returns,
dummy_market_conditions)