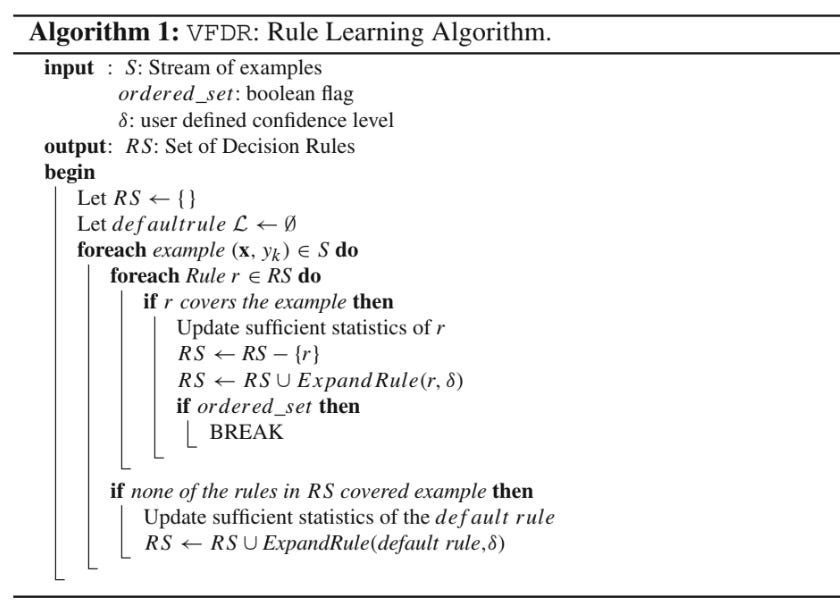
[WITH CODE] Model: Very Fast Decision Rules
Do statistical guarantees hold in unpredictable markets?
Table of contents:
Introduction.
Risks associated with VFDR.
Data stream acquisition and management.
Rule induction and generation in VFDR.
The hoeffding bound and statistical guarantees.
Data simulation and VFDR integration.
Introduction
Sometimes decisions must be made at an unprecedented pace, with prices fluctuating by fractions of a second. Traditional static models can be too slow or cumbersome to adapt to market dynamics. Herein lies the initial dilemma:
how do we construct a framework that not only processes data streams quickly but also adapts its decision rules on the fly, ensuring both speed and accuracy under pressure?
The concept of Very Fast Decision Rules was born from this need—its promise lies in rapidly generating decision rules by dynamically processing streaming data. VFDR is designed to operate under conditions where the data are continuously arriving at high velocities, as seen in modern trading platforms. The algorithm aims to continuously learn and adjust to the trading environment, exploiting minute discrepancies and fleeting arbitrage opportunities before they vanish.
Risks associated with VFDR
While VFDR heralds a new era in adaptive decision-making, it also introduces a set of unique risks:
If the data is not properly curated and transformed, the probability of obtaining overfitting rules is quite high.
VFDR relies on probabilistic guarantees—such as those provided by the Hoeffding bound—to make early decisions. Misestimating these bounds can lead to premature rule acceptance or rejection.
The data streams can be erratic or influenced by external market events. Robust preprocessing and noise filtering become critical to prevent erroneous decisions.
Knowing that, imagine a sudden crash—a moment when market prices plummet superfast due to a cascade of algorithmic triggers. In such a crisis, traditional methods crumble, and VFDR’s potential to adapt and respond rapidly comes into sharp focus.
It is this pivotal event—a market anomaly triggered by the interplay of high-speed trading algorithms—that underscores the necessity for systems capable of ultra-rapid decision-making with strong theoretical guarantees. This moment becomes the driving force behind VFDR research and its prospective application in algorithmic trading frameworks.
You can go deeper in this algorithm by checking this:
We are going to implement a simplified version that includes some changes.
Data stream acquisition and management
Algorithmic trading operates on a relentless torrent of data—each tick, trade, and quote contributes to a vast, ever-flowing river of information. In this environment, VFDR must learn and update its decision rules from a continuous data stream. The challenge begins at the very source: how do we efficiently manage and preprocess this information to feed our algorithm without succumbing to the sheer volume and variability?
Data stream management involves:
Real-Time preprocessing: Filtering out noise and spurious events while preserving relevant market signals.
Incremental updates: Leveraging online learning techniques to update decision rules without having to retrain models from scratch.
Memory and computational constraints: Ensuring that the algorithm runs efficiently within available hardware limitations.
Let us denote the incoming data stream as {x1,x2,…,xt}, where each xi represents a feature vector extracted from market data at time i. The goal is to construct a sequence of decision rules Rt such that the predictive performance P(Rt) is maximized subject to a computation time constraint Tcomp.
In mathematical terms, we can express the VFDR update strategy as:
where ΔRt represents the incremental update based on the new data point xt+1 and Tmax is the maximum allowed processing time per update.
Let’s see an example that simulates real-time data ingestion for our VFDR.
import numpy as np
import time
def simulate_market_data(n_points=1000):
"""Simulate market data as a stream."""
# For illustrative purposes: simulate price changes following a random walk
prices = np.cumsum(np.random.randn(n_points)) + 100
return prices
def preprocess_data(data_point):
"""Simple preprocessing: here, you might filter noise, compute returns, etc."""
# In a real-world scenario, consider using smoothing techniques or anomaly detection
return np.clip(data_point, 0, np.inf)
# Simulate a data stream
data_stream = simulate_market_data(1000)
processed_stream = [preprocess_data(point) for point in data_stream]
# Simulate incremental processing with VFDR (placeholder for decision rule updates)
for idx, data_point in enumerate(processed_stream):
# Simulate processing delay (ideally sub-millisecond in live trading)
time.sleep(0.001)
# Update VFDR model here (not implemented in this simple simulation)
if idx % 100 == 0:
print(f"Processed {idx} data points")This represents a foundational step in handling market data—a prerequisite for any VFDR-based system. Think that this is a toy example, in an actual implementation, the preprocessing function would require more customization for your data and features.
Rule induction and generation in VFDR
At the heart of VFDR lies the ability to construct decision rules rapidly. These rules determine whether to buy, hold, or sell based on specific patterns in the data. The uniqueness of VFDR is its capability to evolve rules in near-real-time by considering both the current market conditions and historical trends.
Imagine a discretionary trader making split-second decisions in a bustling trading floor; VFDR is designed to emulate that intuition by inductively learning rules from the continuous influx of market signals. The underlying challenge is to strike the right balance between decisiveness and prudence.
The process can be broken down into:
Feature Extraction: Selecting pertinent features that capture the essence of market behavior. Examples include price volatility, moving averages, and momentum indicators.
Rule Hypothesis Testing: Given a potential decision rule—e.g., “if the short-term moving average exceeds the long-term moving average, then buy”—the VFDR framework evaluates its performance incrementally.
Adaptive Updating: As new data arrive, the algorithm revises the rule parameters to reflect the evolving market landscape.
To get a clearer idea this pseudo code may be useful:
Consider a rule R represented as a logical expression over market features. The quality Q(R) of a rule can be quantified using a performance metric such as the Gini impurity or information gain. For a binary classification task—e.g., buy or not buy—the information gain IG is defined as:
where:
H(Y) is the entropy of the output variable—trading decision.
N is the total number of instances.
Nv is the number of instances for a given rule value v.
H(Y|R=v) is the conditional entropy of Y given the rule R.
The VFDR algorithm continually computes these quantities in an online manner to decide when a decision rule is statistically significant enough to be deployed in real time.
We can implement the computation of information gain for a simple rule with this:
import numpy as np
def entropy(probabilities):
"""Compute entropy given a list of probabilities."""
return -np.sum([p * np.log2(p) for p in probabilities if p > 0])
def compute_information_gain(rule_outcomes, total_outcomes):
"""
Compute the information gain of a rule.
rule_outcomes: dictionary with keys as rule value and values as count of occurrences
total_outcomes: dictionary with overall outcome counts
"""
total_samples = sum(total_outcomes.values())
overall_entropy = entropy([count / total_samples for count in total_outcomes.values()])
weighted_entropy = 0
for rule_value, count in rule_outcomes.items():
subset_total = count
subset_entropy = entropy([count / subset_total for count in rule_outcomes.values()])
weighted_entropy += (subset_total / total_samples) * subset_entropy
return overall_entropy - weighted_entropy
# Example usage:
total_outcomes = {'buy': 500, 'hold': 300, 'sell': 200}
rule_outcomes = {'buy': 300, 'hold': 100, 'sell': 100}
ig = compute_information_gain(rule_outcomes, total_outcomes)
print(f"Information Gain for the rule is: {ig:.4f}")This provides a simplified glimpse into one of the core components of VFDR: the evaluation and selection of decision rules based on their information gain.
The hoeffding bound and statistical guarantees
One of the key theoretical pillars of VFDR is the Hoeffding bound. This statistical tool provides an upper bound on the difference between the true mean of a random variable and its estimated mean from finite samples. In the context of VFDR, the Hoeffding bound is used to determine the number of observations needed before confidently adopting a decision rule.
The Hoeffding bound states that, for a random variable X bounded by a≤X≤b, after n independent observations, with probability 1−δ the true mean μ is no more than:
In VFDR, let hat μ denote the empirical performance measure—e.g., accuracy or information gain—of a decision rule after nnn samples. The algorithm uses the Hoeffding bound to check whether the difference between the best candidate rule and the second-best candidate is statistically significant. When:
the algorithm can safely commit to R1 as the better decision rule.
This mathematical guarantee allows VFDR to make decisions quickly without requiring the evaluation of every possible rule exhaustively—a critical requirement if you want to face low latency setups.
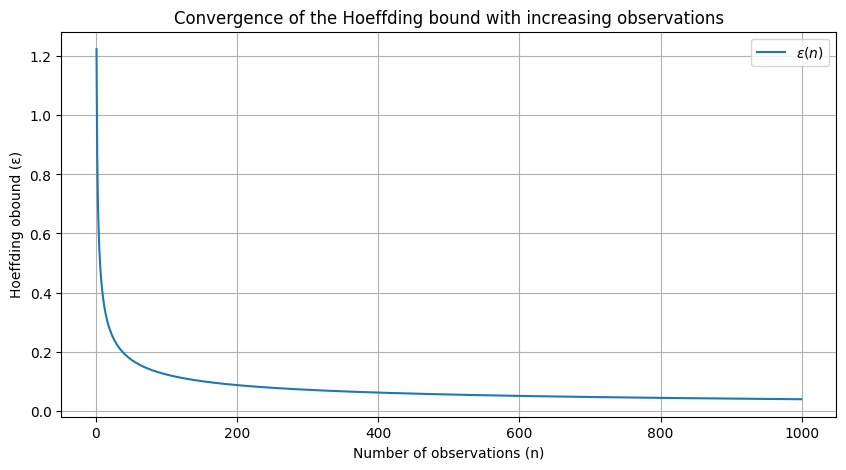
Okay, let’s visualize how the Hoeffding bound ϵ\epsilonϵ decreases as the number of observations nnn increases.
import matplotlib.pyplot as plt
import numpy as np
def hoeffding_bound(n, a=0, b=1, delta=0.05):
return np.sqrt(((b - a) ** 2 * np.log(1 / delta)) / (2 * n))
n_values = np.arange(1, 1000, 1)
epsilon_values = [hoeffding_bound(n) for n in n_values]For this we get:
This plot illustrates that as the number of observations increases, the Hoeffding bound ϵ decreases, thereby reducing the uncertainty associated with rule performance estimates.
The significance of the Hoeffding bound in VFDR cannot be overstated. It is the mathematical linchpin that enables quick decision making by offering a probabilistic guarantee on the performance of a rule. By setting a confidence threshold δ, traders can calibrate the VFDR system to the desired level of risk tolerance. The interplay between n, δ, and the bound ϵ becomes a trade-off between precision and caution—and also speed-acuracy.
Once again you can take a look at the above mentioned through:
Data simulation and VFDR integration
To translate the theory into practice, we will mimic the environment of algorithmic trading. The objective is to integrate VFDR into a live trading simulation that processes real-time data and continuously updates its decision rules.
Imagine a bustling trading floor where every microsecond counts. Our simulation recreates this environment by generating synthetic trading data, processing it through VFDR, and updating decision rules on the fly.
import numpy as np
import matplotlib.pyplot as plt
import time
class VFDRSimulator:
def __init__(self, n_points=1000):
self.n_points = n_points
self.data_stream = self.simulate_market_data(n_points)
self.decision_rules = [] # Placeholder for storing decision rules
def simulate_market_data(self, n_points):
"""Simulate market data: using a random walk process."""
prices = np.cumsum(np.random.randn(n_points)) + 100
return prices
def preprocess_data(self, data_point):
"""Preprocess a single data point."""
# Here, we simply return the data point; real scenarios may involve normalization or filtering.
return max(data_point, 0)
def update_decision_rules(self, data_point, t):
"""
Placeholder for VFDR update:
In a real implementation, this function would evaluate candidate rules
using techniques such as the Hoeffding bound and update the current rules.
"""
# For demonstration, assume a trivial update:
rule_value = np.mean(self.data_stream[:t+1])
self.decision_rules.append(rule_value)
def run_simulation(self):
processed_data = []
for t, data_point in enumerate(self.data_stream):
processed_point = self.preprocess_data(data_point)
processed_data.append(processed_point)
# Simulate VFDR rule update
self.update_decision_rules(processed_point, t)
# Sleep briefly to mimic real-time processing (in practice, this would be near instantaneous)
time.sleep(0.001)
return processed_data, self.decision_rules
# Running the simulation
simulator = VFDRSimulator(n_points=500)
processed_data, decision_rules = simulator.run_simulation()This simulation integrates data preprocessing and dynamic rule updates, offering a glimpse into how VFDR continuously refines its decision-making process in real time.
There are some key performance metrics that need to be considered for any model but specially for VFDR:
Accuracy and precision: Measure the correctness of the generated decision rules.
Latency: The time taken to update rules in response to new data.
Consistency: Stability of decision rules over time, especially under volatile market conditions.
Risk-adjusted return: Incorporation of risk metrics such as the Sharpe ratio to evaluate performance.
False positive/negative rates: Balancing the trade-offs between overly conservative and overly aggressive decisions.
The final technical point addresses the integration of VFDR into existing algorithmic trading systems. Given the fast-paced and high-stakes environment of trading floors, VFDR must meld seamlessly with other components such as execution engines, order management systems, and real-time analytics dashboards.
class TradingSystem:
def __init__(self):
self.vfdr = VFDRSimulator(n_points=1000)
self.order_book = [] # Simplified representation
self.trade_log = []
def run_trading_session(self):
processed_data, decision_rules = self.vfdr.run_simulation()
for t, price in enumerate(processed_data):
# Simple trading logic based on VFDR decision rule
rule_value = decision_rules[t]
if price > rule_value:
self.execute_trade("buy", price, t)
else:
self.execute_trade("sell", price, t)
def execute_trade(self, action, price, time_tick):
trade = {"action": action, "price": price, "time": time_tick}
self.order_book.append(trade)
self.trade_log.append(trade)
print(f"Trade executed: {trade}")
def summarize_trades(self):
# Summarize trade log to compute basic performance metrics
num_buys = sum(1 for trade in self.trade_log if trade['action'] == "buy")
num_sells = sum(1 for trade in self.trade_log if trade['action'] == "sell")
print(f"Total Buys: {num_buys}, Total Sells: {num_sells}")
# Running the integrated trading system simulation
trading_system = TradingSystem()
trading_system.run_trading_session()
trading_system.summarize_trades()Here is where we get the rules itself:
In non-toy examples, such modules would be connected with sophisticated order routing and risk management systems.
Now, today I'm going to give you some homework. I want you to create a hybrid model, better risk filters for this model, and transform the data into a format that's easily digestible for the model and doesn't incur overfitting. I won't go into scalability because I know the above already requires quite a bit of work.
PS: Which of these features do you think is most important for stock picking?
This is an invitation-only access to our QUANT COMMUNITY, so we verify numbers to avoid spammers and scammers. Feel free to join or decline at any time. Tap the WhatsApp icon below to join
Appendix
Full script:
import numpy as np
import matplotlib.pyplot as plt
import time
# -----------------------------------------------------------
# Section 1: Market Data Simulation and Preprocessing Functions
# -----------------------------------------------------------
def simulate_market_data(n_points=1000):
"""
Simulate market data as a random walk process.
"""
prices = np.cumsum(np.random.randn(n_points)) + 100
return prices
def preprocess_data(data_point):
"""
Preprocess a single data point by ensuring it is non-negative.
In real scenarios, more complex filtering can be applied.
"""
return max(data_point, 0)
# -----------------------------------------------------------
# Section 2: VFDR Simulator Class for Decision Rule Updates
# -----------------------------------------------------------
class VFDRSimulator:
def __init__(self, n_points=1000):
self.n_points = n_points
self.data_stream = simulate_market_data(n_points)
self.decision_rules = [] # Placeholder for storing dynamic decision rules
def preprocess_data(self, data_point):
"""Apply preprocessing to a single data point."""
return preprocess_data(data_point)
def update_decision_rules(self, data_point, t):
"""
A simplified update: compute the average of all data seen so far as the rule value.
In a real VFDR, candidate decision rules would be evaluated using the Hoeffding bound.
"""
rule_value = np.mean(self.data_stream[:t+1])
self.decision_rules.append(rule_value)
def run_simulation(self):
"""
Process the data stream incrementally and update the decision rules.
Returns both the processed data and the decision rule evolution.
"""
processed_data = []
for t, data_point in enumerate(self.data_stream):
processed_point = self.preprocess_data(data_point)
processed_data.append(processed_point)
self.update_decision_rules(processed_point, t)
# Simulate a very brief delay for real-time processing (adjust as needed)
time.sleep(0.001)
return processed_data, self.decision_rules
# -----------------------------------------------------------
# Section 3: Information Gain Computation Functions
# -----------------------------------------------------------
def entropy(probabilities):
"""
Compute entropy given a list of probabilities.
"""
return -np.sum([p * np.log2(p) for p in probabilities if p > 0])
def compute_information_gain(rule_outcomes, total_outcomes):
"""
Compute the information gain of a decision rule.
- rule_outcomes: dictionary with keys as outcomes and values as counts under the rule.
- total_outcomes: dictionary with overall outcome counts.
"""
total_samples = sum(total_outcomes.values())
overall_entropy = entropy([count / total_samples for count in total_outcomes.values()])
weighted_entropy = 0
for rule_value, count in rule_outcomes.items():
subset_total = count
# Compute the entropy for the subset (using the same distribution for simplicity)
subset_entropy = entropy([count / subset_total for count in rule_outcomes.values()])
weighted_entropy += (subset_total / total_samples) * subset_entropy
return overall_entropy - weighted_entropy
# -----------------------------------------------------------
# Section 4: Statistical and Visualization Tools
# -----------------------------------------------------------
def hoeffding_bound(n, a=0, b=1, delta=0.05):
"""
Compute the Hoeffding bound for a given number of observations.
"""
return np.sqrt(((b - a) ** 2 * np.log(1 / delta)) / (2 * n))
def plot_hoeffding_bound():
"""
Visualize how the Hoeffding bound (ε) decreases with more observations.
"""
n_values = np.arange(1, 1000, 1)
epsilon_values = [hoeffding_bound(n) for n in n_values]
plt.figure(figsize=(10, 5))
plt.plot(n_values, epsilon_values, label=r"$\epsilon(n)$")
plt.xlabel("Number of observations (n)")
plt.ylabel("Hoeffding Bound (ε)")
plt.title("Convergence of the Hoeffding Bound with Increasing Observations")
plt.legend()
plt.grid(True)
plt.show()
# -----------------------------------------------------------
# Section 5: Sharpe Ratio Calculation and Evolution Simulation
# -----------------------------------------------------------
def sharpe_ratio(returns, risk_free_rate=0.01):
"""
Compute the Sharpe ratio for a series of returns.
"""
excess_returns = returns - risk_free_rate
mean_excess = np.mean(excess_returns)
std_excess = np.std(excess_returns)
if std_excess == 0:
return 0.0
return mean_excess / std_excess
def simulate_sharpe_evolution(n_points=500):
"""
Simulate the evolution of the Sharpe ratio over time.
"""
sharpe_values = []
for i in range(2, n_points):
returns = np.random.normal(0.001, 0.02, i)
sharpe_values.append(sharpe_ratio(returns))
return sharpe_values
def plot_sharpe_evolution():
"""
Plot the simulated evolution of the Sharpe ratio.
"""
sharpe_evolution = simulate_sharpe_evolution(500)
plt.figure(figsize=(10, 5))
plt.plot(sharpe_evolution, label="Evolving Sharpe Ratio")
plt.xlabel("Time (ticks)")
plt.ylabel("Sharpe Ratio")
plt.title("Risk Evaluation: Evolution of the Sharpe Ratio")
plt.legend()
plt.grid(True)
plt.show()
# -----------------------------------------------------------
# Section 6: Trading System Integration Simulation
# -----------------------------------------------------------
class TradingSystem:
def __init__(self):
self.vfdr = VFDRSimulator(n_points=1000)
self.order_book = [] # Simple order book representation
self.trade_log = []
def run_trading_session(self):
"""
Run the simulation of a trading session using VFDR-generated decision rules.
Simple trading logic: if the price is above the rule value, execute a "buy", else "sell".
"""
processed_data, decision_rules = self.vfdr.run_simulation()
for t, price in enumerate(processed_data):
rule_value = decision_rules[t]
if price > rule_value:
self.execute_trade("buy", price, t)
else:
self.execute_trade("sell", price, t)
return processed_data, decision_rules
def execute_trade(self, action, price, time_tick):
"""
Log the trade and print a confirmation.
"""
trade = {"action": action, "price": price, "time": time_tick}
self.order_book.append(trade)
self.trade_log.append(trade)
print(f"Trade executed: {trade}")
def summarize_trades(self):
"""
Summarize and output basic trade statistics.
"""
num_buys = sum(1 for trade in self.trade_log if trade['action'] == "buy")
num_sells = sum(1 for trade in self.trade_log if trade['action'] == "sell")
print(f"Total Buys: {num_buys}, Total Sells: {num_sells}")
# -----------------------------------------------------------
# Section 7: Main Function to Run All Simulations and Plots
# -----------------------------------------------------------
def main():
# 1. Run VFDR simulation and plot market data with decision rule evolution.
simulator = VFDRSimulator(n_points=500)
processed_data, decision_rules = simulator.run_simulation()
plt.figure(figsize=(12, 6))
plt.plot(processed_data, label="Processed Price")
plt.plot(decision_rules, label="VFDR Decision Rule", linestyle='--')
plt.xlabel("Time (ticks)")
plt.ylabel("Price / Rule Value")
plt.title("VFDR Simulation: Market Data and Evolving Decision Rule")
plt.legend()
plt.grid(True)
plt.show()
# 2. Plot the Hoeffding bound convergence.
plot_hoeffding_bound()
# 3. Compute and display an example of information gain.
total_outcomes = {'buy': 500, 'hold': 300, 'sell': 200}
rule_outcomes = {'buy': 300, 'hold': 100, 'sell': 100}
ig = compute_information_gain(rule_outcomes, total_outcomes)
print(f"Information Gain for the rule is: {ig:.4f}")
# 4. Plot the Sharpe ratio evolution.
plot_sharpe_evolution()
# 5. Run the trading system simulation and summarize trade activity.
trading_system = TradingSystem()
processed_data_trading, decision_rules_trading = trading_system.run_trading_session()
trading_system.summarize_trades()
if __name__ == "__main__":
main()










Hi QuantBeckman! Would you consider this VFDR-based approach suitable for true high-frequency trading (HFT), where latencies are in the microsecond range and execution requires colocated infrastructure? Or is it more aimed at fast but mid-frequency algorithmic strategies (e.g., every few seconds)?
Are you currently running this VFDR-based decision-making framework in live trading systems, or is it more of a conceptual/experimental prototype at this stage?