Table of contents:
Introduction.
Risk and limitations of time bars.
Introducing information-driven bars.
Range bars.
Renko bars.
Filter bars.
Volatility bars.
Introduction
You are observing the markets in real-time—thousands of price ticks cascading across your screen, each reflecting a momentary shift in supply, demand, and sentiment. At first glance, the data appears evenly spaced, structured, and regular. Yet beneath this surface lies a deeper asymmetry: the rhythm of market activity is not governed by the uniform cadence of the wall clock, but by the irregular pulses of information flow and volatility.
This distinction underscores a fundamental challenge in financial data sampling: the dissonance between chronological time and what might more aptly be termed market time. While traditional time bars—such as 1-minute or 5-minute intervals—offer simplicity and compatibility with standard backtesting frameworks, they assume that each unit of time carries equal informational weight. The reality, however, is far more complex.
Markets are event-driven. Activity and volatility are not uniformly distributed. A 5-minute interval during a low-liquidity midday lull is not equivalent to a 5-minute window during a central bank announcement. Yet both are treated identically in time-based sampling. This can lead to misleading signals, particularly for strategies sensitive to volatility regimes or order flow.
Moreover, time bars introduce well-known statistical complications. Volatility clustering results in periods of extreme variability being aggregated in the same temporal units as periods of calm, producing heteroskedastic return series that impair the performance of risk models, signal generation algorithms, and machine learning architectures. For example, attempts to train predictive models on such unevenly informative data may yield unstable or overfit outcomes.
Alternative approaches, such as tick bars, volume bars, and dollar bars, aim to address these shortcomings by redefining sampling based on market activity rather than elapsed time. Tick bars group a fixed number of trades, adapting to bursts of market engagement. Volume bars aggregate data until a fixed number of shares or contracts have changed hands. Dollar bars go further, normalizing across instruments by aggregating based on the notional value traded. These methods tend to produce more statistically stable returns and better align with the flow of market information. Check about these bars here:
Ultimately, selecting an appropriate sampling method is not a matter of convenience—it is a design decision that shapes the behavior, accuracy, and robustness of a trading strategy. While time-based bars remain common, their limitations should not be overlooked. Today we'll be reviewing a completely different type of bar, some of which are quite common and popular among traders.
Risk and limitations of time bars
Moving beyond time-based bars is a quest for a more intelligent market clock, one that ticks not with the passage of seconds, but with the occurrence of meaningful events. The idea is to sample observations not when the clock dictates, but when the market does something interesting. This leads us to the concept of information-driven bars, where each bar represents a consistent quantum of information, however that might be defined–a certain price movement, a specific volume traded, or a particular amount of capital changing hands.
But this path is no sunlit meadow; it is a labyrinth, riddled with multiple obstacles. The very flexibility that makes these bars appealing also introduces complexity.
How much price movement constitutes a "meaningful event"?
How large should a "brick" of price change be?
What level of volatility warrants a new bar?
These questions throw the algorithmic trader into the murky waters of parameter selection, a domain where the siren song of overfitting constantly plays. Furthermore, the irregular arrival of these bars in clock time can make traditional time-series analysis techniques more challenging to apply directly, requiring new perspectives on concepts like duration and seasonality.
Traditional time-based bars—e.g., 1-minute, 1-hour—are the historical default. They sample price data at fixed temporal intervals. While simple to compute and understand, their core flaw lies in the assumption that market activity is uniformly distributed across time. This is demonstrably false. Markets exhibit periods of high and low activity, and time-based bars treat these identically.
Consider two 5-minute bars:
Bar A (low activity): Price meanders within a tight range. The bar captures minimal information, potentially just noise.
Bar B (high activity): A news event causes price to surge and plummet. The bar captures a significant trend and volatility, but crams it into the same temporal box as Bar A.
This disparity leads to several issues for algorithmic models:
The variance of returns is not constant across bars. Statistical models assuming homoskedasticity will be misspecified.
The distribution of returns from time-based bars often exhibits excess kurtosis—fat tails—and skewness, deviating from the normal distribution assumed by many financial models.
During low activity, time bars accumulate noise. During high activity, crucial intraday details within the fixed interval can be lost or averaged out.
The illusion is that we are measuring the market; in reality, we are often just measuring the clock, forcing market behavior into an arbitrary temporal grid. The quest, therefore, is to find sampling methods that adapt to the market's rhythm, not an external one.
Introducing information-driven bars
Information-driven bars, or event-based bars, are constructed based on the flow of information rather than the passage of time—What matters here is what we consider information.. The goal is to create bars that each represent a similar amount of "market eventfulness." This synchronicity aims to produce a bar series with more desirable statistical properties, such as returns that are closer to being independently and identically distributed and, ideally, closer to a normal distribution.
The fundamental premise is that significant market events—price changes, volume surges, volatility spikes—are what truly matter. By forming bars based on these events, we let the market itself dictate the sampling frequency. When the market is frenetic, bars form rapidly, capturing the action. When the market is placid, bars form slowly, patiently waiting for meaningful information. This dynamic sampling is the hallmark of price-movement bars.
The following Python snippet outlines a base class structure that has been developed by Hudson and Thames and we are going to use to build all the bars. Furthermore, it can be used to implement various types of information-based toolbars, not just those popularized by López de Prado. This illustrates the common framework before diverging into specific event triggers.
from abc import ABC, abstractmethod
import pandas as pd
import numpy as np
from collections import deque
def _batch_chunks(df, size):
"""
Split DataFrame into equal-sized chunks for batch processing.
"""
idx = np.arange(len(df)) // size
return [grp for _, grp in df.groupby(idx)]
class BaseBars(ABC):
def __init__(self, metric=None, batch_size=int(2e7)):
self.metric = metric
self.batch_size = batch_size
self.reset()
def reset(self):
self.open = self.high = self.low = self.close = None
self.prev_price = None
self.tick_rule = 0
self.stats = dict(cum_ticks=0, cum_dollar=0, cum_vol=0, cum_buy_vol=0)
def _sign(self, price):
if self.prev_price is None:
diff = 0
else:
diff = price - self.prev_price
self.prev_price = price
if diff != 0:
self.tick_rule = np.sign(diff)
return self.tick_rule
def run(self, rows):
bars = []
for t, p, v in rows:
self.stats['cum_ticks'] += 1
self.stats['cum_dollar'] += p * v
self.stats['cum_vol'] += v
if self._sign(p) > 0:
self.stats['cum_buy_vol'] += v
# initialize OHLC
if self.open is None:
self.open = self.high = self.low = p
# update
self.high = max(self.high, p)
self.low = min(self.low, p)
self.close = p
# check threshold
self._check_bar(t, p, bars)
return bars
def batch_run(self, data, to_csv=False, out=None):
cols = ['date', 'tick', 'open', 'high', 'low', 'close',
'vol', 'buy_vol', 'ticks', 'dollar']
bars = []
if isinstance(data, pd.DataFrame):
chunks = _batch_chunks(data, self.batch_size)
else:
chunks = pd.read_csv(data, chunksize=self.batch_size, parse_dates=[0])
for chunk in chunks:
bars.extend(self.run(chunk[['date', 'price', 'volume']].values))
df = pd.DataFrame(bars, columns=cols)
df['date'] = pd.to_datetime(df['date'])
df.set_index('date', inplace=True)
if to_csv and out:
df.to_csv(out)
return df
@abstractmethod
def _check_bar(self, t, p, bars):
...This BaseBars class elegantly provides a common engine for accumulating tick data and delegates the crucial decision of when to form a bar to its children. This is the dawn of designing our own market clocks.
Range bars
Range bars are among the conceptually simplest price-movement bars. A new bar is formed when the price range (High - Low, or more commonly |Close - Open| of the forming bar) exceeds a predefined threshold, R.
The condition to close a RangeBar k when observing tick i is:
where openk is the open price of the current bar being built, and closei is the current tick's price.
The allure of range bars is their promise of uniformity in price movement per bar. Each bar, by definition, represents a price journey of at least R. This can help normalize price fluctuations, making subsequent analyses like volatility estimation or pattern recognition more consistent.
If you'd like to dig a little deeper, check out this PDF. I liked its approach:
Here's how the RangeBars class implements this logic, inheriting from BaseBars:
class RangeBars(BaseBars):
def __init__(self, threshold, batch_size=int(2e7)):
super().__init__(None, batch_size)
self.threshold = threshold
def _check_bar(self, t, p, bars):
if self.open is None:
return
if abs(self.close - self.open) >= self.threshold:
bars.append([pd.to_datetime(t), self.stats['cum_ticks'],
self.open, self.high, self.low, self.close,
self.stats['cum_vol'], self.stats['cum_buy_vol'],
self.stats['cum_ticks'], self.stats['cum_dollar']])
self.reset()The _check_bar method is the heart here. Once the price stretches sufficiently from its opening point, a bar is "born," and the process resets, waiting for the next R-sized journey. The challenge, of course, is choosing an appropriate R. Too small, and you're swamped with noisy bars. Too large, and you miss crucial subtleties.
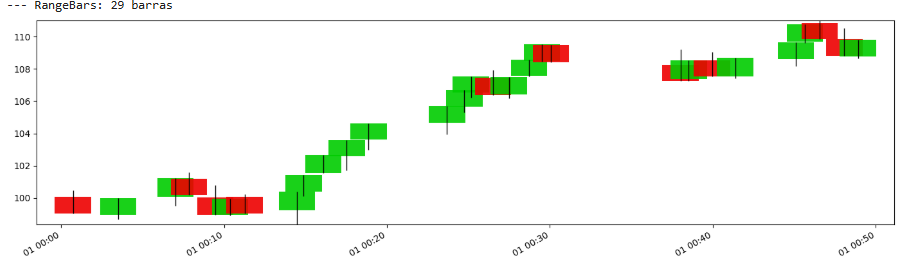
Let’s see:
During high volatility, many such bars would form in a short clock-time period, while in low volatility, fewer bars would form over a longer clock-time period.
Advantages:
Each bar—ideally—represents a consistent amount of price excursion. This can help normalize price action.
More bars will form during periods of high price movement—volatility—and fewer during quiet periods, naturally focusing sampling where the action is.
The fixed range can sometimes help in identifying mini support and resistance levels defined by the range quantum R.
By requiring a minimum price movement, some of the smaller, less significant price jitters might be filtered out compared to time bars in quiet markets.
Disadvantages:
The choice of the range threshold R is critical and often data-specific—instrument, market conditions. An inappropriate R can lead to too many—noisy—bars or too few—loss of detail.
Bars do not close at fixed time intervals, which can complicate time-based analysis or comparisons with time-based indicators.
If the market is choppy but the overall price movement frequently crosses the R threshold back and forth without establishing a trend, range bars can still generate many signals that lead to whipsaws.
If price enters a very tight consolidation phase, much smaller than R, bar formation can slow dramatically or halt, potentially missing subtle accumulation/distribution patterns.
Renko bars
Renko bars, originating from Japan—like Candlesticks—offer a unique way to visualize price movements and identify trends by filtering out minor fluctuations. They consist of "bricks" of a predefined fixed size, B. A new brick is added only when the price moves by at least B from the closing price of the last brick. If the price moves by B in the current direction, a new brick of that color—e.g., green for up, red for down—is added. Critically, for a reversal—a brick of the opposite color—the price often needs to move 2B in the opposite direction—one B to negate the current brick's direction and another B to form the new one. The provided code implements a simpler version where any B movement forms a new brick.
The condition is: Each time cumulative price movement Δp since the last brick's close hits the brick size B, a new brick is emitted.
The RenkoBars class implementation:
class RenkoBars(BaseBars):
def __init__(self, brick_size, batch_size=int(2e7)):
self.last_close = None
super().__init__(None, batch_size)
self.brick_size = brick_size
def reset(self):
super().reset()
if self.last_close is not None:
self.open = self.high = self.low = self.close = self.last_close
def _check_bar(self, t, p, bars):
if self.last_close is None:
self.last_close = p
diff = p - self.last_close
direction = np.sign(diff)
num = int(abs(diff) // self.brick_size)
for _ in range(num):
o = self.last_close
c = o + direction * self.brick_size
bars.append([pd.to_datetime(t), self.stats['cum_ticks'],
o, max(o, c), min(o, c), c,
self.stats['cum_vol'], self.stats['cum_buy_vol'],
self.stats['cum_ticks'], self.stats['cum_dollar']])
self.last_close = c
super().reset()
self.open = self.high = self.low = self.close = cRenko bars excel at highlighting trends—a series of same-colored bricks—and support/resistance levels. Their clean, decluttered appearance can be a breath of fresh air, but the abstraction of time means two consecutive bricks could have formed seconds or hours apart. The choice of B is, again, paramount.
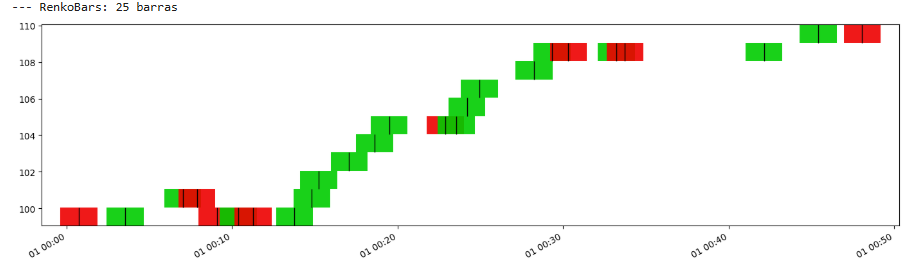
Let’s see:
As you can see, both the Renko and Range are very similar. In fact, the Renko is quieter.
Advantages:
Renko bars provide a very clear representation of trends by filtering out minor price fluctuations. A series of same-colored bricks is a strong trend signal.
By focusing only on price movements of at least size B, Renko bars effectively eliminate noise and small corrections against the trend.
Horizontal lines of bricks often clearly indicate support and resistance levels.
The uniform brick size and removal of time make bars patterns and trendlines very distinct.
Disadvantages:
The brick size B is crucial. Too small, and the bars becomes noisy; too large, and it lags significantly, missing finer details and entry/exit points.
Especially with classic Renko requiring a 2B move for a reversal, signals can be delayed, leading to late entries or exits.
Renko bars do not show the exact highs and lows within a time period, only whether a brick was formed. All price action that doesn't result in a new brick is ignored.
The time axis is completely irregular. Two consecutive bricks could have formed seconds, minutes, or even hours apart, making time-based analysis impossible directly on Renko bars.
How gaps are handled can vary, and large opening gaps can distort the initial brick formation.
Filter bars
Filter bars, sometimes known as Constant percentage bars or Log-price bars—though the latter is more specific—aim to form new bars when the price moves by a certain percentage, θ, from a base price, pbase. This pbase is typically the closing price of the last formed bar or the open of the current bar.
The condition is:
where pi is the current price.
This type of bar is interesting because a fixed percentage move means different absolute price changes depending on the current price level. A 1% move at $10 is $0.10, while at $1000 it's $10. This can be more appropriate for assets whose volatility scales with price.
The FilterBars implementation:
class FilterBars(BaseBars):
def __init__(self, threshold_pct, batch_size=int(2e7)):
super().__init__(None, batch_size)
self.threshold_pct = threshold_pct
self.base = None
def reset(self):
super().reset()
self.base = None
def _check_bar(self, t, p, bars):
if self.base is None:
self.base = p
move = abs(p - self.base) / self.base if self.base != 0 else 0
if move >= self.threshold_pct:
bars.append([pd.to_datetime(t), self.stats['cum_ticks'],
self.open, self.high, self.low, p,
self.stats['cum_vol'], self.stats['cum_buy_vol'],
self.stats['cum_ticks'], self.stats['cum_dollar']])
self.reset()Filter bars dynamically adjust the absolute price change required to form a new bar, making them potentially more robust across different price regimes or assets with varying price magnitudes. The key obstacle remains the judicious selection of θ.
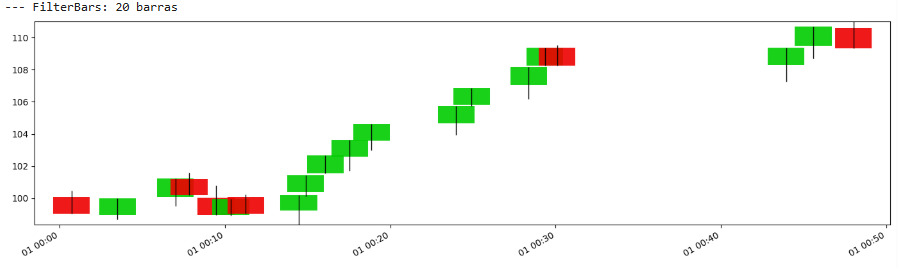
Let’s plot this:
And once again, there is not much difference with the previous ones.
Advantages:
A fixed percentage move accounts for the fact that a $1 move is more significant for a $10 stock than for a $1,000 stock. This makes the bars comparable across different price levels or for assets whose volatility differs.
Each bar represents a similar percentage change, which can be more meaningful for certain strategies that focus on relative value or log-return–based signals.
As the price increases, the absolute price change required to form a new bar also increases—and vice versa. In other words, when prices are higher, each bar needs a larger dollar-amount move to trigger.
Disadvantages:
The choice of the percentage threshold θ is critical and needs careful calibration.
The behavior can subtly change depending on whether pbase is the bar's open, previous close, or another reference.
Like other information-driven bars, they do not form at fixed time intervals.
If θ is set appropriately for higher price levels, it might still be too small for very low-priced, volatile assets, leading to many bars. Conversely, if set for low-priced assets, it might be too insensitive at high price levels.
Extreme sensitivity if pbase is very small.
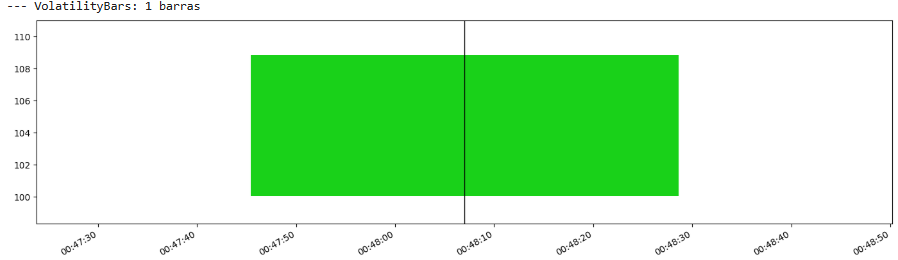
Volatility bars
Volatility bars take a more direct approach to synchronizing with market conditions. A new bar is formed when the observed volatility over a certain lookback window W—of ticks or time, though typically ticks for consistency with the bar type—exceeds a predefined volatility threshold σ.
The condition is:
Here, s is the standard deviation of prices over the most recent W ticks.
This method directly addresses the issue of changing market temperament. When volatility is high, s will reach σ more quickly, leading to faster bar formation. When volatility is low, bar formation slows down. This ensures that each bar, in a sense, represents a similar amount of surprise or risk.
The VolatilityBars implementation:
class VolatilityBars(BaseBars):
def __init__(self, vol_threshold, window, batch_size=int(2e7)):
# initialize window first so reset can clear it
self.window = deque(maxlen=window)
super().__init__(None, batch_size)
self.vol_threshold = vol_threshold
def reset(self):
super().reset()
self.window.clear()
def _check_bar(self, t, p, bars):
self.window.append(p)
if len(self.window) == self.window.maxlen:
vol = float(np.std(np.array(self.window)))
if vol >= self.vol_threshold:
bars.append([pd.to_datetime(t), self.stats['cum_ticks'],
self.open, self.high, self.low, self.close,
self.stats['cum_vol'], self.stats['cum_buy_vol'],
self.stats['cum_ticks'], self.stats['cum_dollar']])
self.reset()Volatility bars are intuitively appealing because they directly adapt to one of the most critical aspects of market behavior. However, they introduce two parameters to tune: W and σ. The choice of W determines the responsiveness of the volatility estimate, while σ sets the sensitivity for bar creation.
Let’s see:
Wait, what!? 😕 Few amount of data guys, this one sucks…
Advantages:
Bars naturally form faster when the market is volatile and slower when it's calm. This aligns sampling with market "eventfulness" or risk.
Each bar attempts to capture a similar amount of realized volatility or surprise.
Can lead to a bar series where quantities like the number of ticks per bar or the duration of bars have better statistical properties for modeling.
Useful for strategies that need to behave differently in high-volatility versus low-volatility regimes.
Disadvantages:
Requires setting both the lookback window W for the volatility calculation and the volatility threshold σ. This increases the complexity of optimization and the risk of overfitting.
While standard deviation is common, other volatility estimators could be used, each with its own properties and impact.
The lookback window W introduces some lag in the volatility estimation. A shorter window is more responsive but noisier; a longer window is smoother but slower to react.
Common to all information-driven bars and besides, it samples too slow.
Okay, the resolutions offered by Range, Renko, Filter, and Volatility bars are interesting. They address the core issue of time-based sampling's inability to distinguish between periods of intense activity and quietude.
By design, these bars aim to achieve more stable statistical properties—closer to IID, normality of returns. This allows for the more reliable application of statistical learning models and risk management frameworks that often carry assumptions violated by raw time-series data. The curse of heteroskedasticity is, if not lifted, significantly mitigated.
Instead of passively listening at fixed intervals, algorithms using these bars engage in a dynamic dialogue. They sample when the market "speaks" with conviction. This adaptability can lead to quicker reactions to emerging trends and a reduction in being whipsawed by noise during consolidation. It’s the difference between a scheduled check-up and an emergency response system.
Features engineered on these more uniform informational units—e.g., momentum over N information-bars, volatility of N information-bars—can be more robust and comparable across different market regimes than features built on time bars that encapsulate vastly different amounts of activity.
The conclusions here are:
There is no universal "best" bar type.
The optimal choice is contingent upon the specific asset class, the trading strategy's horizon and logic, and the market microstructure.
A trend-following strategy might favor Renko for its clarity, while a breakout strategy might lean towards Range or Volatility bars.
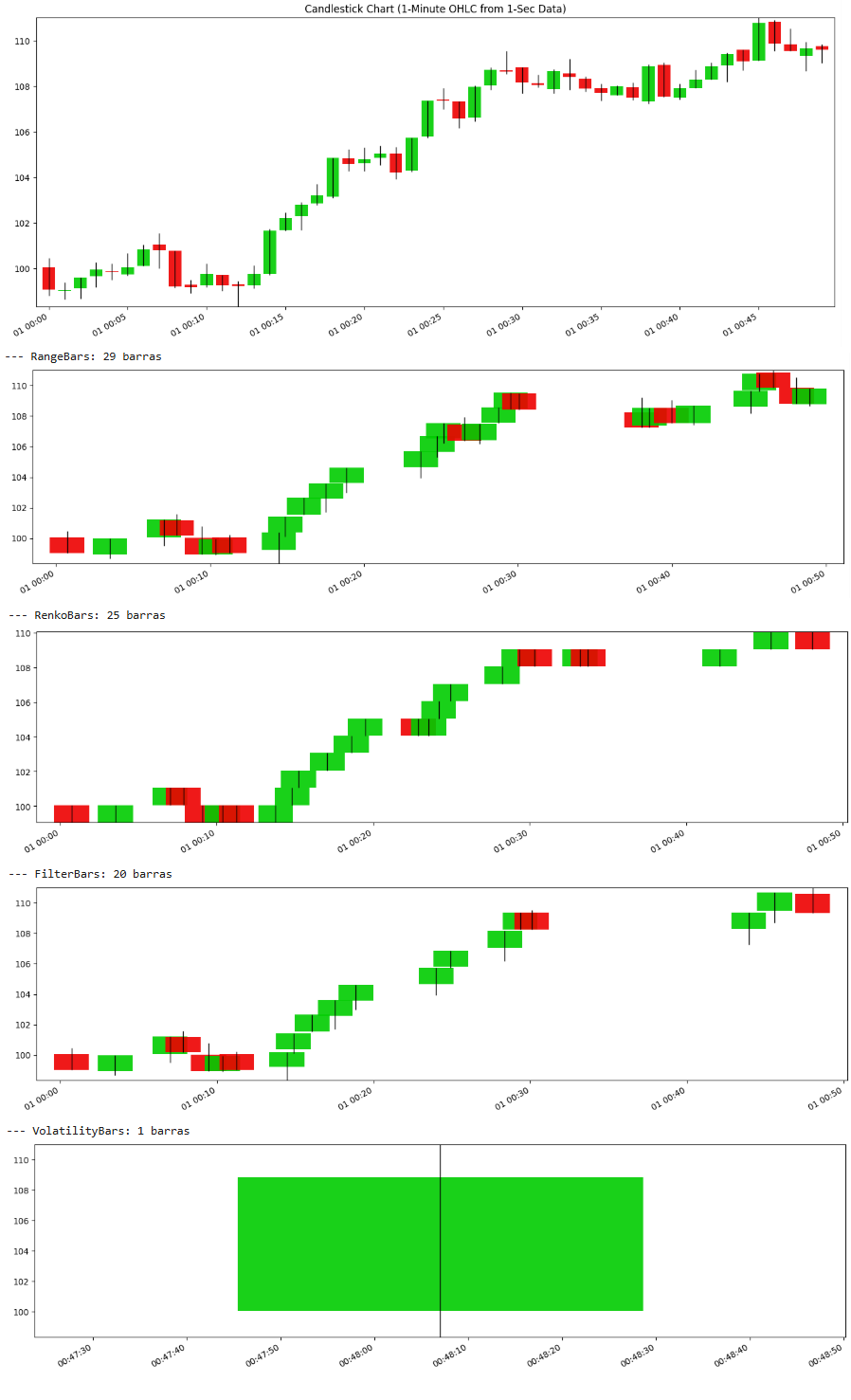
Let's make a final comparison visually:
Apart from the volatility bar, which samples very slowly, the rest yield fairly similar results—at least visually. In the next issue—this was part 2/3—we’ll dive deeper from a statistical perspective.
Okay team! Great job today! It’s time to switch off. Stay curious, stay boundless, stay quanty! 🕹️
PS: Of the ones we’ve seen so far, which one would you go with?
This is an invitation-only access to our QUANT COMMUNITY, so we verify numbers to avoid spammers and scammers. Feel free to join or decline at any time. Tap the WhatsApp icon below to join








I am testing $bats at the moment, but « run bars » (inspired by MLdP) is on my radar.