[WITH CODE] Market Making: Avellaneda–Stoikov model

Can you manage inventory—or is it managing you? Optimizing every microsecond of exposure

---

Table of contens:

1. Introduction.

2. Limitations from Avellaneda-Stoikov framework.

3. Algorithmic architecture.

4. Optimal quotes.

5. Inventory management dynamics.

6. Avellaneda-Stoikov Implementation.

7. Model improvements and lines of research.

---

Introduction

Alright, let’s break this down like we’re chatting over coffee. You know how market making feels? It’s like playing high-speed whack-a-mole in a casino where the moles are microseconds, and the casino’s on fire. Your job? Be the guy who’s always shouting “I’ll buy!” and “I’ll sell!” at the same time, pocketing the spread—that tiny gap between bid and ask. Sounds simple, right? Nah. It’s a brutal game of razor-thin margins and oh crap moments.

Here’s the kicker: you want that spread as wide as possible to cash in, but go too wide and nobody trades with you. You’re just yelling into the void. Too tight? Congrats, you’re now the exit liquidity for every algo shark with a faster connection. And that’s just the warm-up.

Let’s talk risks. First up, directional risk. Imagine you buy 10,000 shares of Stock X at 50, planning to flip them quick at 50.05. But then earnings drop, and suddenly it’s tanking to $48. Now you’re stuck holding a bag of regret. Classic. Then there’s inventory risk—you’re supposed to stay neutral, like a Switzerland of liquidity. But sometimes you end up long or short, sweating bullets because every tick feels like a heart attack. It’s like juggling chainsaws while balancing on a yoga ball.

And don’t get me started on adverse selection. You post a juicy ask price, thinking you’re slick, but some HFT fratboy front-runs you, sniffing out a market move you didn’t see. Now your safe quote is a liability. Oh, and volatility? When markets go haywire, your models start crying.

So how do you survive? Back in the day, it was all gut instinct and superstition—like trading on a horoscope. Then Avellaneda-Stoikov dropped in 2008 and changed the game. Finally, math to the rescue! They turned market making into an optimization problem: balance inventory risk against spread profit, using stochastic calculus.

But Avellaneda-Stoikov has quite a few mistakes. In fact, I started discussing this topic with a colleague following a request from a subscriber. And today I'm bringing you some of the notes. I don't want to be too hard on the math, but there are indices everywhere these days.

Limitations from Avellaneda-Stoikov framework

Think of the basic Avellaneda–Stoikov model as a beautifully crafted blueprint for a theoretical airplane. It shows the perfect aerodynamic shape, the ideal engine size. But to actually fly it, you need to contend with real-world wind gusts, turbulence, fuel impurities, and the fact that your passengers aren't dimensionless points. These limitations are the real-world factors that challenge the ideal flight plan.

Let's break down these friction points:

1. Unrealistic model assumptions:

   • The model assumes random, independent order fills. In reality, orders cluster and influence each other, making fill probabilities less predictable than the model assumes.

   • Prices are modeled as smoothly random with fixed volatility. But markets have volatile periods that jump and cluster, leading to inaccurate risk estimates and potentially mistimed quotes.

   • The model assumes your trading doesn't affect the market price—But if you can afford to do market making, you will probably affect the price.. Large trades actually move the market against you, a crucial cost the basic model ignores.

2. Parameter calibration challenges:

   • Pinpointing how order flow responds to your quote distance is complex, requiring analysis of noisy, high-speed data, and these parameters aren't stable.

   • The model assumes your tolerance for risk is constant. This can lead to suboptimal choices; ideal strategies might require adapting risk levels.

   • The model uses a basic curve for how fill probability drops with distance. Real market depth is more complex, making the model's spread calculations less precise.

3. Microstructure limitations:

   • Markets have minimum price steps and orders are filled in sequence at each price. The continuous model ignores these, missing key factors affecting execution probability and speed.

   • The model overlooks the cost of trading, which eats into profits and makes theoretical spreads appear more lucrative than they are.

   • The model assumes instantaneous order placement. Delays expose quotes to informed traders who can exploit outdated prices before you can react.

You can go deeper by reviewing this paper from Avellaneda & Stooikov (2006):

High-frequency trading in a limit order book

188KB ∙ PDF file

Download

Download

In short, it's not a model to use for the average person, I want to make this clear. But at the same time, I would like to have a chat with you to learn about your lines of work in this dynamic inventory control. Because at the end of the day, trading is about these two things:

• Pricing.

• Inventory.

Algorithmic architecture

At the heart of the Avellaneda–Stoikov model beats the concept of the reservation price r. This is not simply the observed market mid-price S, but rather the market maker's own, adjusted internal valuation of the asset. Think of it as your personal equilibrium point, a reference from which you calculate your willingness to buy or sell. What adjusts this internal compass? Your inventory q.

The formula is elegantly simple yet profoundly insightful:

\(r = S - q \,\gamma\, \sigma^2 \,(T - t)\)

Let's unpack this. The current market mid-price is the starting point. The subsequent term, −qγσ²(T−t), is the inventory risk adjustment.

• q: Your current inventory. If q>0, you are long; if q<0, you are short.

• γ: Your risk aversion parameter. This is your personal knob for how much pain inventory imbalance causes you. A higher γ means you really dislike holding inventory.

• σ²: The volatility of the asset price. Higher volatility means the price can swing more wildly, making your current inventory position riskier.

• (T−t): The time remaining until the end of your trading horizon. As time runs out, the urgency to flatten your position increases, making inventory risk more potent.

The negative sign in front of the adjustment term is crucial. If you are long, this term is negative, pushing your reservation price down. Why? Because you want to sell your excess inventory. By lowering your internal perceived value, you signal your willingness to sell at a price lower than the current market mid-point, incentivizing buyers. Conversely, if you are short, the term −qγσ²(T−t) becomes positive—negative times negative—pushing your reservation price up. You want to buy back your short position. A higher reservation price indicates a willingness to buy at a price higher than the market mid-point, attracting sellers.

This dynamic adjustment of the reservation price based on inventory is the model's core mechanism for steering you back towards a neutral inventory state, acting like a self-correcting feedback loop.

Optimal quotes

Another important point here is the optimal quotes. Once the reservation price is established, the optimal bid and ask quotes are derived. These quotes represent the prices at which the market maker is willing to transact, symmetrically placed around the reservation price but influenced by market dynamics beyond simple mid-point deviations.

The formulas are:

\(b = r - \delta,\quad a = r + \delta\)

Where δ is the optimal half-spread, calculated as:

\(\delta = \frac{1}{\gamma}\, \log\!\Bigl(1 + \frac{\gamma}{k}\Bigr) + \frac{1}{2}\,\gamma\,\sigma^2\,(T - t)\)

Here, k is a parameter related to the intensity of order arrivals. It captures how likely you are to get an order execution based on how far your quote is from the mid-price. A higher k suggests that even small price differences can attract orders.

Let's dissect δ:

• The term 1/γ​log(1+γ/k​) is related to the profitability of capturing the spread. It shows that a higher order arrival intensity or lower risk aversion allows for a narrower spread while still attracting trades.

• The term 1/2​γσ²(T−t) is the inventory risk component of the spread. Notice its similarity to the reservation price adjustment. As time runs out or volatility increases, this term grows, widening the optimal spread. Why? To compensate you for the increased risk of holding inventory if a trade doesn't happen.

So, the optimal spread a−b=2δ is not fixed. It's a dynamic entity that widens as inventory risk increases—higher γ, σ², or time remaining—and also depends on market depth/order arrival rates. By quoting b=r−δ and a=r+δ, the market maker is setting prices that maximize their expected utility—balancing profit from spread captures against the cost/risk of holding inventory—over the remaining time horizon.

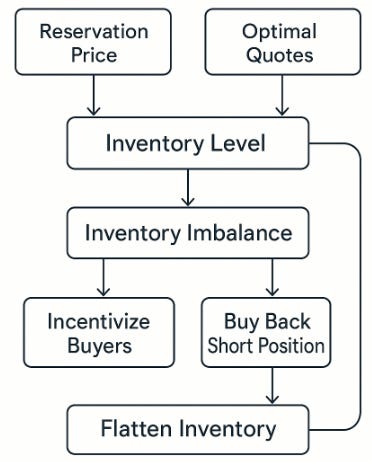
Inventory management dynamics

The model essentially turns inventory management into a feedback control system. Your current inventory level is the system's state variable, and the reservation price and optimal quotes are the control signals designed to steer that state towards zero.

Imagine inventory as a boat's ballast. Too much ballast on one side—long inventory— and the boat lists, becoming unstable. The market maker's strategy, guided by the lower reservation price and willingness to sell, is to effectively jettison some of that ballast by incentivizing buyers. Conversely, too little ballast or ballast skewed to the other side—short inventory—and the boat lists the other way. The strategy then shifts to buying back the short position.

The beauty is in the dynamic nature. The pressure to flatten inventory isn't constant; it intensifies as the end of the trading horizon approaches. As (T−t) shrinks, the inventory risk adjustment still depends on q, γ, and σ², but the multiplier of that risk (T−t) decreases. However, simultaneously, the risk component of the spread also shrinks, potentially narrowing the spread based on this component. This creates a nuanced interplay. While the per-unit inventory pain might feel less intense as time runs out, the urgency to flatten before the horizon ends— t=T, where the model assumes inventory must be zeroed out or its value is simply q×S—means the quotes will still aggressively try to attract offsetting trades if inventory is significantly non-zero.

The model implicitly pushes for higher trading volume when inventory is imbalanced and time is running out, even if it means quoting slightly less profitable prices relative to the mid-point. This constant push and pull—between seeking profitable spreads and managing inventory risk—is the core dynamic orchestrated by the reservation price.

Avellaneda-Stoikov Implementation

Quants have developed sophisticated variations that address some of these issues, incorporating jump-diffusion processes for prices, more detailed order book dynamics, and transaction costs. Nevertheless, the basic Avellaneda–Stoikov framework provides the essential conceptual bedrock upon which these more complex models are built.

Let’s code it in its basic form:

class AvellanedaStoikovMarketMaker:
    def __init__(self, 
                 sigma: float,      # Market volatility (σ)
                 kappa: float,      # Order‐book liquidity parameter (κ)
                 gamma: float,      # Inventory risk aversion (γ)
                 A: float,          # Baseline arrival intensity
                 T: float           # Time horizon (e.g. normalized to 1)
                ):
        """
        Initialize model parameters and histories.
        """
        self.sigma = sigma
        self.kappa = kappa
        self.gamma = gamma
        self.A = A
        self.T = T
        self.inventory = 0.0
        self.cash = 0.0
        
        # Histories for tracking
        self.time_history = []
        self.inventory_history = []
        self.pnl_history = []

    def reservation_price(self, mid_price: float, t: float) -> float:
        """
        Compute inventory‐skewed reference price.
        """
        return mid_price - self.inventory * self.gamma * self.sigma**2 * (self.T - t)

    def optimal_total_spread(self, t: float) -> float:
        """
        Compute the total optimal spread.
        """
        term1 = self.gamma * self.sigma**2 * (self.T - t)
        term2 = (2.0 / self.gamma) * math.log(1.0 + self.gamma / self.kappa)
        return term1 + term2

    def get_quotes(self, mid_price: float, t: float) -> (float, float):
        """
        Generate bid and ask quotes.
        """
        r = self.reservation_price(mid_price, t)
        delta = self.optimal_total_spread(t) / 2.0
        bid = r - delta
        ask = r + delta
        return bid, ask

    def arrival_intensity(self, delta: float) -> float:
        """
        Exponential arrival intensity for orders at distance δ.
        """
        return self.A * math.exp(-self.kappa * delta)

    def simulate_step(self, mid_price: float, t: float, dt: float):
        """
        Simulate one time step dt, update histories.
        """
        bid, ask = self.get_quotes(mid_price, t)
        delta_bid = mid_price - bid
        delta_ask = ask - mid_price

        # Fill probabilities
        p_buy  = self.arrival_intensity(delta_bid) * dt
        p_sell = self.arrival_intensity(delta_ask) * dt

        # Random fills
        if random.random() < p_buy:
            self.inventory += 1
            self.cash -= bid

        if random.random() < p_sell:
            self.inventory -= 1
            self.cash += ask

        # Record histories
        self.time_history.append(t)
        self.inventory_history.append(self.inventory)
        self.pnl_history.append(self.cash + self.inventory * mid_price)

    def pnl(self, current_price: float) -> float:
        """
        Mark‐to‐market P&L.
        """
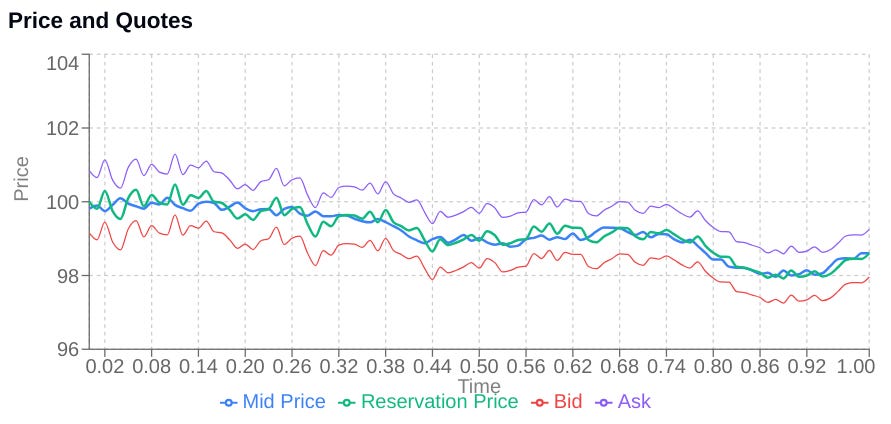
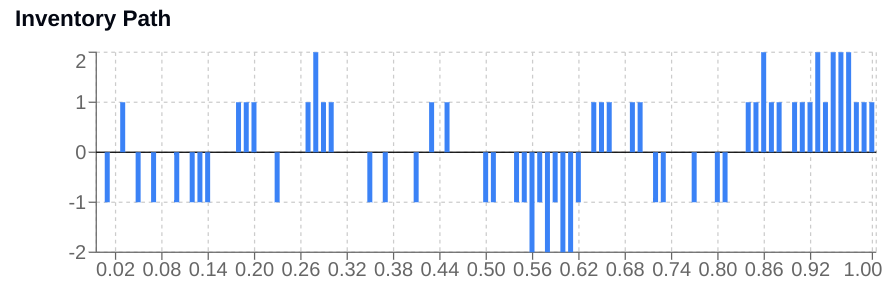
        return self.cash + self.inventory * current_price

Let’s see what this gives us:

Oh! mmm 🧐 this smells weird to me guys. Besides, every tick, every order filled, every second that passes requires a recalculation. These updates need to happen in the realm of micros—better with nanos, so get your FPGA up and running.

The core equations themselves are not computationally intractable, but the sheer volume of calculations across hundreds or thousands of instruments, coupled with a demanding technical environment, is.

Model improvements and lines of research

Okay, let's move on to some of the potential improvements discussed. These are just potential lines of research yet, So there could be mistakes and certainly a lot of room for improvement, okay? So here the notes!

Mathematically, each core formula in Avellaneda–Stoikov is upgraded in four ways:

1. State‐dependent parameters.

2. Price‐impact term.

3. Fees & ticks.

4. Inventory bounds.

So! Grab a pen and paper, let's look at a more realistic and sensible frame:

• Risk-aversion:

  \(\begin{aligned} &\text{Original:} &&\gamma(t) = \gamma,\\ &\text{Enhanced:}&&\gamma_{\rm dyn}(t) = \gamma_0\Bigl[1 + \bigl(I(t)/I_{\max}\bigr)^2\Bigr]. \end{aligned}​\)

  γ is no longer a constant. You scale it up as your inventory moves closer to its hard limit. A trader with near‐zero inventory can afford to quote tight and chase P&L. But once you’ve bought or sold a lot, you’re exposed, so you become more risk-averse, widening spreads to discourage further accumulation and protecting against big adverse moves.

• Volatility and liquidity:​​​

  \(\begin{aligned} &\text{Original:} &&\sigma,\;\kappa\;\text{fixed},\\ &\text{Enhanced:}&& \begin{cases} \sigma_{\rm est}^2(t) = \lambda\,\sigma_{\rm est}^2(t-1) + (1-\lambda)\bigl(\Delta\ln p\bigr)^2,\\[4pt] \kappa_{\rm est}(t) = \begin{cases} \lambda\,\kappa_{\rm est}(t-1) + (1-\lambda)\,\dfrac1{\mathrm{avg\ fills}},&\text{if fills}>0,\\ \kappa_{\rm est}(t-1),&\text{otherwise.} \end{cases} \end{cases} \end{aligned}​\)

  We replace a static volatility with an exponentially‐weighted moving average of squared log‐returns. Quick to react to volatility spikes and slow to forget them—ensuring your quoted spread expands in choppy markets and tightens when things calm down.

• Reservation price:

  \(\begin{aligned} &\text{Original:} && r_{\rm orig}(t) = p_m(t)\;-\;I(t)\,\gamma\,\sigma^2\,(T-t),\\[4pt] &\text{Enhanced:} && r_{\rm enh}(t) = p_m(t) - I(t)\,\gamma_{\rm dyn}(t)\,\sigma_{\rm est}^2(t)\,(T-t) - \eta\,\frac{I(t)}{I_{\max}}. \end{aligned}\)

  Here sou subtract or add a small penalty proportional to your current inventory. Real trades on big sizes push the market. By nudging your reference price away from the mid when your position skews, you simulate that impact: you sell slightly below mid when long—so you don’t chase your own price up—and buy slightly above when short.

• Optimal spread:

  \(\begin{aligned} &\text{Original:} && \Delta_{\rm orig}(t) = \gamma\,\sigma^2\,(T-t) + \frac{2}{\gamma}\,\ln\!\Bigl(1 + \frac{\gamma}{\kappa}\Bigr),\\[4pt] &\text{Enhanced:} && \Delta_{\rm enh}(t) = \gamma_{\rm dyn}(t)\,\sigma_{\rm est}^2(t)\,(T-t) + \frac{2}{\gamma_{\rm dyn}(t)}\, \ln\!\Bigl(1 + \frac{\gamma_{\rm dyn}(t)}{\kappa_{\rm est}(t)}\Bigr) + 2\,\mathrm{fee}. \end{aligned}​\)

  A flat fee per executed trade is added to the spread formula. Exchanges charge fees or pay rebates. Ignoring these can turn a seemingly profitable strategy into a loser once you pay commissions. By building fees into your quoting, you ensure each round‐trip covers its cost.

• Bid/ask quotes:

  \(\begin{aligned} &\text{Original:} && \begin{cases} \mathrm{Bid} = r_{\rm orig} - \tfrac12\Delta_{\rm orig},\\ \mathrm{Ask} = r_{\rm orig} + \tfrac12\Delta_{\rm orig}, \end{cases}\\[6pt] &\text{Enhanced:} && \begin{cases} \mathrm{Bid} = \displaystyle\mathrm{round}\!\Bigl(\tfrac{r_{\rm enh}-\Delta_{\rm enh}/2}{\tau}\Bigr)\,\tau,\\ \mathrm{Ask} = \displaystyle\mathrm{round}\!\Bigl(\tfrac{r_{\rm enh}+\Delta_{\rm enh}/2}{\tau}\Bigr)\,\tau, \end{cases} \quad \text{and if } I\ge I_{\max}\Rightarrow\text{no Bid, } I\le -I_{\max}\Rightarrow\text{no Ask.} \end{aligned}​\)

  Quotes are rounded to the nearest tick and totally suppressed on one side once you hit ±I_max​. Markets trade in discrete price increments. Rounding avoids quoting impossible prices. Prevents runaway positions. Once you hit your pre-set inventory limit, you stop buying or selling altogether until you reduce your position.

• Arrival intensity:

  \(\begin{aligned} &\text{Original:} && \lambda(\delta) = A\,e^{-\kappa\,\delta},\\[4pt] &\text{Enhanced:} && \lambda_{\rm enh}(\delta) = A_0\,e^{-\kappa_{\rm est}(t)\,\delta}, \quad p = \min\{1,\;\lambda_{\rm enh}(\delta)\,\Delta t\}. \end{aligned}​\)

  You cap the arrival probability p=λ Δt at 1 and only update κ when you actually see fills. Without a cap, a large λ or big Δt can produce probabilities > 1, which is nonsensical. Only adjusting κ on real fills prevents noise spikes when zero fills would otherwise drive κ to astronomical values and shut down trading.

The first results of some prototypes are incredibly crazy, really. Typical when surgery is practically free and you even get paid for it 😮‍💨

Too good, the quality is directly proportional to the execution speed: “<5 nanos + 0 commissions == constant profit.”

Well, it's been a while since I started writing this, and the guy I mentioned earlier came up with a bombshell... and that is that many of the blunders I've encountered persist:

• The assumption that fills are independent may still sneak in.

• Dynamic adjustments can overcorrect if inventory reversals happen rapidly.

• If you're quoting multiple correlated assets treating inventory independently per symbol can lead to systemic directional exposure.

• Because inventory-based loss builds up gradually and fills come probabilistically, a market maker may look profitable short-term but accumulate latent directional exposure that leads to large corrections.

• Overfitting in parameter adaptation.

Oh man, my chest slowly sinks with every word I exchange with this guy 🥲

Alright, alright, I see those hungry minds craving another round—but we’re clocking out here. Killer execution, team! Hope this fires up your models and hacks the game harder.

Unplug today! Reset your buffers, calibrate those latent features, and let volatility fuel your next exploit. Keep your algorithms adaptive, your portfolio antifragile, and your curiosity unbounded. Stay sharp, stay quant⚡

PS: Do you think it makes sense to use ML methods with this level of latency?