Table of contents:
Introduction.
Architectural elements of position sizing.
Quantitative signal analysis.
Volatility-responsive calibration.
Portfolio correlation architecture.
Exit valuation mechanics.
Strategic deployment patterns.
Minimal position deployment protocol.
Maximum position deployment protocol.
Aggressive allocation dynamics.
Execution and framework integration.
Geometric position scaling.
Capital-risk calibration matrix.
Moderate-opportunity impact assessment.
Algorithmic positioning.
Optimization framework.
Integration of temporal dimensions.
Continuous recalibration mechanisms.
RiskOps paradigm.
Introduction
Algorithmic traders face a perpetual paradox: How much capital should be committed to each opportunity? This isn't merely a question of numbers—it's the fundamental tension that defines successful algorithmic trading strategies.
Imagine yourself standing at the edge of a vast financial market, algorithms humming beneath your feet, each one scanning millions of price movements per second. Your trading system has detected a promising signal—perhaps a statistical anomaly in the futures market or a fleeting correlation pattern across currency pairs. The question that follows is deceptively simple yet profoundly consequential: how much of your capital should you deploy?
This decision—position sizing—represents the fulcrum upon which algorithmic trading success balances. Too timid, and even the most brilliant strategy yields negligible returns. Too aggressive, and a single market hiccup can devastate your capital base. Worse still, the optimal answer shifts continuously as market conditions evolve.
The risks lurking within this decision matrix are manifold:
Allocation imbalance risk: Deploying excessive capital to correlated assets, potentially magnifying losses during sector-wide movements.
Volatility misjudgment risk: Failing to adjust position sizes appropriately as market turbulence changes.
Exit opportunity risk: Insufficient consideration of how quickly positions can be unwound in various market conditions.
Signal confidence miscalibration: Over-allocating to weaker signals or under-allocating to high-conviction opportunities.
The pivotal moment that crystallizes this dilemma often arrives without fanfare—perhaps when an algorithm encounters its first genuine market crisis, or when a previously reliable signal suddenly falters across multiple assets simultaneously. This critical juncture forces a fundamental reassessment of how position sizing decisions are made within the algorithmic framework.
Architectural elements of position sizing
Position sizing in algorithmic trading is far more than a simple fixed percentage or a static rule applied uniformly across all opportunities. Instead, in systemaric approaches, it represents a dynamic and critical architectural layer, weaving together multiple quantitative and contextual factors to determine the optimal capital allocation for each trade at any given moment. This complex interplay of variables dictates not just what to trade, but how much, fundamentally shaping the risk profile and return potential of the entire portfolio.
Quantitative signal analysis
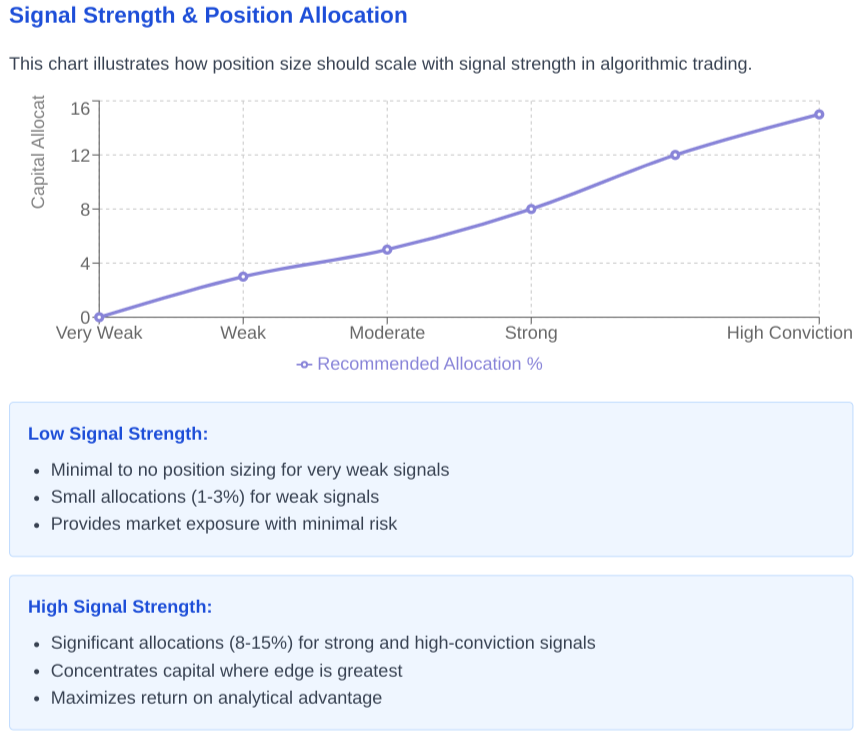
At the heart of position sizing lies the algorithm's capacity to quantify its own edge. The strategy advantage—a mathematical representation of the algorithm's statistical edge—serves as the primary regulator of trading frequency. Like a master conductor determining the tempo of a symphony, this dictates the rhythm of market engagement.
High-conviction represents moments when the algorithm detects particularly strong signals—perhaps when multiple independent factors align in perfect mathematical harmony. During these rare convergences, the algorithm may justifiably increase position sizes, much as a poker player might raise significantly when holding a royal flush.
The dynamic relationship between these advantages creates an algorithmic tension: when to maintain consistent position sizes versus when to amplify capital deployment in response to exceptional opportunities.
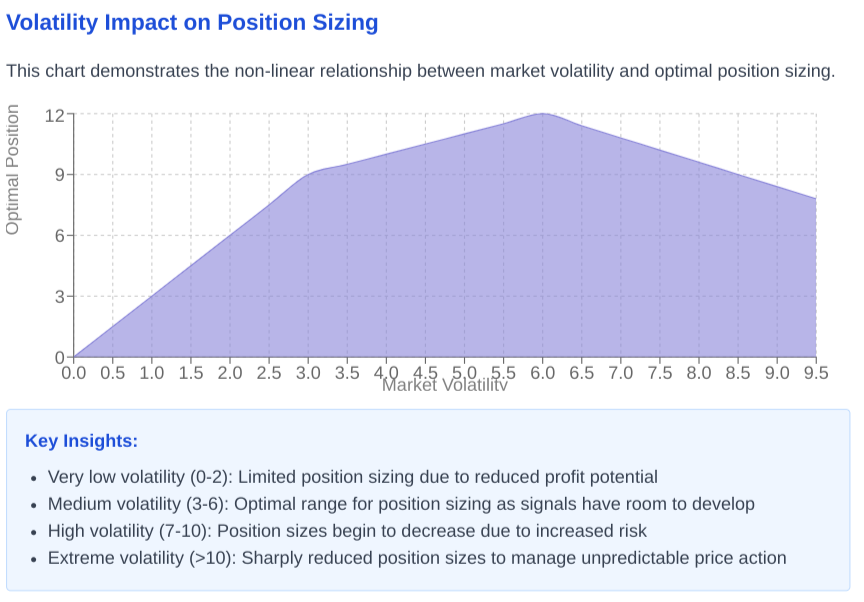
Volatility-responsive calibration
Market volatility acts as both threat and opportunity—a dualistic force requiring response mechanisms. Consider the algorithm as a sailor navigating treacherous waters:
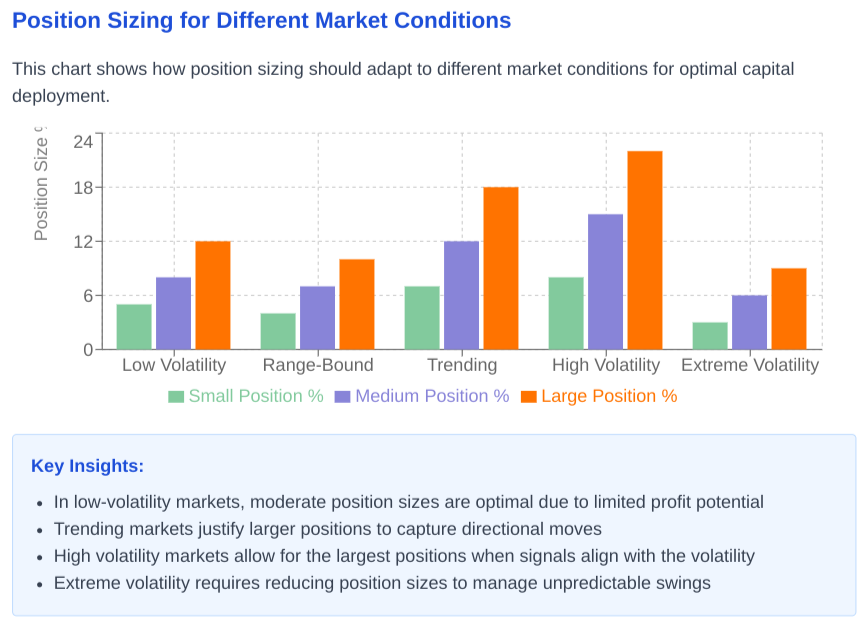
In calm seas—low-volatility markets—smaller sails—position sizes—suffice, as dramatic progress is unlikely. In moderate winds—trending markets—larger sails capture more energy. But when storms rage—extreme volatility—sail area must be reduced again to prevent capsizing.
This sailing metaphor illustrates the non-linear relationship between volatility and optimal position sizing—a relationship that many algorithmic systems fail to properly encode, creating exploitable inefficiencies for more competitors.
Portfolio correlation architecture
The number of correlated assets within the portfolio creates a complex mathematical relationship affecting individual position sizes. As correlation increases, the effective risk concentration intensifies, even when nominal position sizes remain constant.
Imagine a multi-dimensional chess game where each piece's movement affects the vulnerability of others. An algorithm must maintain awareness of these invisible connections, dynamically adjusting individual position sizes as correlation structures evolve—often imperceptibly to human observers.
Exit valuation mechanics
The value of exit opportunity introduces a fascinating temporal dimension to position sizing. This concept quantifies the expected utility of terminating positions under various market conditions.
When the potential value of rapid position exit is low—perhaps in a range-bound market where quick directional moves are improbable—smaller positions become optimal. Conversely, when exit value is high—during trend formation phases or volatility breakouts—larger positions may capture greater value, provided appropriate risk constraints remain in place.
This dynamic exit valuation creates a feedback loop within algorithms, allowing them to modify position sizes not just based on entry conditions, but on expected exit scenarios—a form of temporal arbitrage invisible to other systems.
Strategic deployment patterns
Effective position sizing extends beyond calculating the optimal allocation for a single trade; it involves adopting overarching strategic deployment patterns that dictate the aggregate approach to capital allocation based on prevailing market conditions, the nature of available trading opportunities, and the portfolio's current state.
Rather than applying a monolithic sizing rule, algorithms dynamically select from distinct deployment protocols, each designed to optimize outcomes under specific circumstances:
This strategic layer ensures that the algorithm's capital is not merely allocated, but deployed in a manner aligned with the immediate tactical needs and long-term objectives, ranging from prioritizing capital preservation in uncertain times to aggressively pursuing growth during periods of exceptional opportunity.
Minimal position deployment protocol
Small position sizes become optimal under specific market conditions and signal configurations. These situations represent scenarios where capital preservation takes precedence over aggressive growth, creating a conservative deployment pattern focused on longevity rather than explosive returns.
The algorithm may adopt minimal position sizing when:
Market signals suggest potential adverse movements of significant magnitude.
The strategy detects few high-return opportunities relative to risk.
Quick position exit would provide minimal value—low exit opportunity value.
The portfolio contains numerous moderate-potential positions requiring protection.
High-conviction opportunities are scarce.
Markets exhibit strong range-bound characteristics.
The algorithm detects high-probability but low-magnitude opportunities.
Market volatility reaches extreme levels, exceeding historical calibration parameters.
Strong mean-reversion patterns dominate price action.
Counter-trend strategies appear dominant among market participants.
Each of these conditions creates a mathematical environment where capital preservation through position size restriction optimizes the algorithm's long-term expectancy, even at the cost of immediate profit potential.
Maximum position deployment protocol
Conversely, large position sizes become optimal when market conditions and signal quality align to create exceptional opportunities. These represent moments when the algorithm can justifiably concentrate capital to maximize return potential while maintaining acceptable risk parameters.
The algorithm may implement maximum position sizing when:
Signals indicate minimal potential for adverse price movement—like Trump news.
Numerous high-quality opportunities present favorable return-to-risk ratios.
Rapid exit would provide substantial value—high exit opportunity value.
The strategy detects multiple high-conviction signals simultaneously.
The algorithmic framework naturally focuses on high-magnitude price movements.
Dynamic or trending markets create substantial directional bias.
Protection against unfavorable reversals remains cost-effective.
Strong directional signals align with favorable market structure.
Market conditions decisively favor the algorithm's strategic approach.
Few moderate-potential trades compete for capital allocation.
These conditions create an environment where concentrated capital deployment optimizes expected returns without excessive risk exposure—the algorithmic equivalent of pressing a strong advantage.
Aggressive allocation dynamics
Under certain specialized conditions, algorithms may adopt particularly aggressive sizing strategies that temporarily exceed normal risk parameters. These situations typically arise when:
A substantial portion of existing positions show profit relative to most potential market movements.
Future adverse movements threaten to erode these unrealized gains.
High-conviction positions face vulnerability to sudden market structure shifts.
This creates a temporal arbitrage opportunity—a window where aggressive sizing captures value before market conditions deteriorate. Such opportunities often close quickly, requiring algorithmic responses too rapid for manual intervention.
Execution and framework integration
Translating the strategic decisions regarding position size into actual market exposure requires execution methodologies and seamless integration within the broader portfolio management framework. This involves not only determining the theoretical optimal size but also structuring the way capital is deployed, managed, and constrained relative to the total capital base and the existing portfolio composition.
These architectural elements address the practical challenges of implementing position sizing rules, ensuring that theoretical allocations are translated into effective market positions while respecting overall risk limits and maximizing capital efficiency.
Geometric position scaling
Geometric position sizing represents a capital allocation approach where consistent percentage deployment occurs across sequential signals or trades to reach target allocation. This mathematical progression creates a form of averaging in that captures optimal entry points without requiring perfect timing precision.
This approach becomes particularly powerful when:
The algorithm detects strong directional bias.
Capital can be maximized across successful sequential trades.
Strong initial signals justify early allocation with confirming signals expanding position size.
Market participants demonstrate primarily reactive rather than anticipatory behavior.
Geometric sizing creates a mathematical progression represented as G1, G2, G3, etc., where the numeral indicates the number of entry points across which the total allocation is distributed. Each approach optimizes for different market conditions and signal types, creating a flexible deployment framework that adapts to evolving conditions.
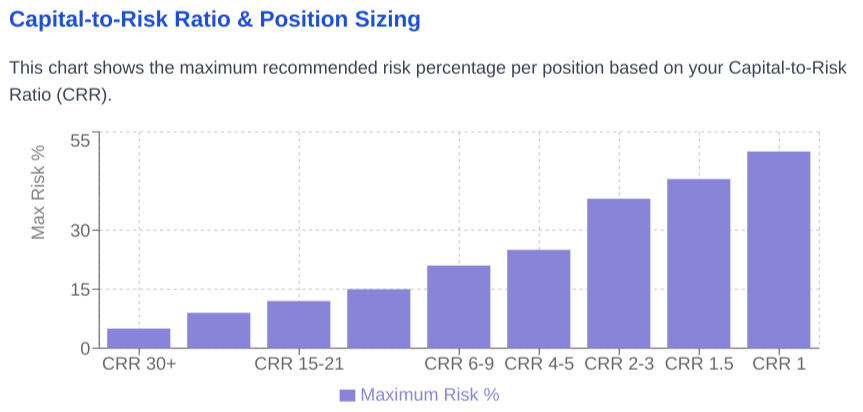
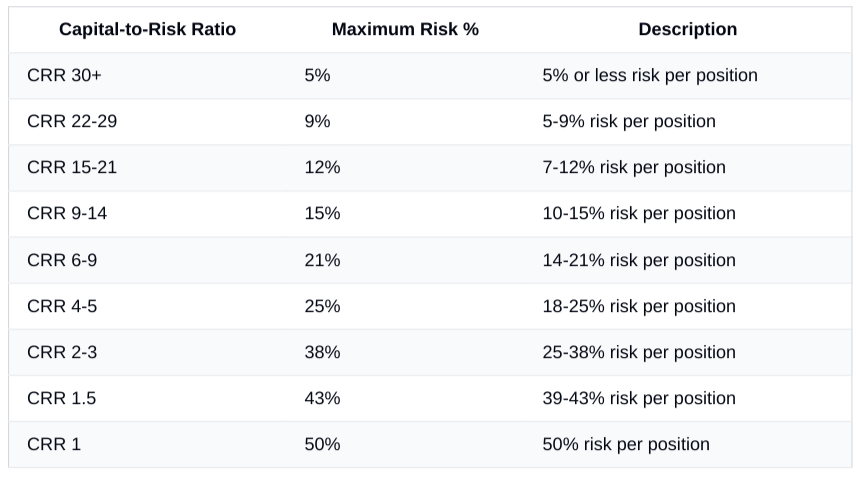
Capital-risk calibration matrix
The Capital-to-Risk ratio creates a mathematical framework for determining appropriate risk exposure relative to total capital. This relationship generates a non-linear risk allocation pattern where:
Large capital bases (CRR 30+) justify minimal risk per position (≤5%)
Moderate capital bases (CRR 9-14) support medium risk per position (10-15%)
Limited capital bases (CRR 1-3) require substantial risk per position (25-50%)
This mathematical relationship creates exploitable inefficiencies when competing algorithms fail to properly calibrate their risk parameters relative to their capital base. An algorithm can identify these mismatches through market microstructure analysis, potentially exploiting competitors who deploy inappropriate position sizes for their capital constraints.
Moderate-opportunity impact assessment
Moderate-potential trades create an anchorage effect on high-conviction opportunities within the portfolio. As moderate-probability positions accumulate, they constrain optimal sizing for exceptional opportunities due to aggregate risk constraints.
This creates an intriguing mathematical tension where:
Algorithms with fewer moderate-potential trades enjoy greater flexibility in high-conviction sizing
Counter-trend positioning becomes viable when competing algorithms hold diverse moderate-potential positions
Subsequent position expansion requires confirmation or rapid exit
Strategic allocation to moderate opportunities must be carefully constrained to preserve capital for exceptional signals
This relationship explains why many algorithms underperform despite occasionally identifying exceptional opportunities—their capital becomes inefficiently allocated across too many moderate-potential positions, restricting their ability to capitalize on rare high-conviction signals.
Algorithmic positioning
Moving beyond static rules and even dynamic adjustments based solely on current conditions, advanced algorithmic position sizing represents a continuous, multi-dimensional optimization process.
At this level, algorithms not only calculate optimal sizing based on a multitude of inputs but also integrate temporal dynamics, anticipate future market states, and continuously refine their sizing parameters through feedback loops.
This approach views position sizing not as a single decision point, but as an ongoing state of calibration, where capital allocation is an active component of the overall trading strategy, adapting and evolving in real-time.
Optimization framework
Here some examples of the basic dimensions to incorporate in the problem any quant should model:
Strategy metrics across varying timeframes
Volatility response functions calibrated to market regimes
Correlation structures within the portfolio asset universe
Exit opportunity valuation across potential market scenarios
Capital-to-risk ratios appropriate to the available capital base
Distribution of high-conviction versus moderate-potential signals
Geometric allocation patterns across sequential entry points
This framework creates a decision-making process more complex than the binary large versus small paradigm suggests. Some algorithms dynamically recalibrate across this multi-dimensional space, continuously optimizing position sizes as conditions evolve.
Integration of temporal dimensions
Perhaps most fascinating is how algorithms incorporate temporal dimensions into position sizing. They evaluate not just current signal quality, but how signals might evolve, how exit opportunities might change, and how competing algorithms might respond to emerging market structures.
This creates a form of game-theoretic positioning where algorithms anticipate the reactions of other market participants, adjusting position sizes to capitalize on expected behavior patterns. Such temporal integration represents the frontier of algorithmic position sizing—moving beyond static rules to dynamic, anticipatory capital deployment.
Continuous recalibration mechanisms
The most advanced algorithms implement continuous feedback loops that recalibrate position sizing parameters based on performance metrics. This creates an evolutionary optimization process where successful sizing patterns receive increased allocation while underperforming patterns see reduced deployment.
This machine learning approach to position sizing creates algorithms that adapt to changing market regimes without requiring explicit reprogramming—a form of algorithmic adaptation that mirrors biological evolution but occurs at computational speed.
RiskOps paradigm
What emerges here is not merely a set of rules but an integrated framework that dynamically adjusts to market conditions, signal quality, and portfolio composition.
The fundamental drivers of position sizing decisions include:
The quantifiable edge of the algorithm across different market conditions
The temporal value of position exit under various scenarios
The capital-to-risk relationship that defines sustainable allocation
The distribution between high-conviction and moderate-potential opportunities
These elements combine to create a decision matrix where optimal position sizes continuously evolve. Perhaps most intriguing is how these position sizing principles create exploitable opportunities. When competing algorithms consistently missize their positions and they create inefficiencies that more systems can capitalize upon.
Okay, time to wrap things up. We've worked really hard today, team! So that's all for today.
Tomorrow we sharpen the edge even more—refactor your code, stress-test your signals, and let the data speak louder than the hype. May your drawdowns be brief and your Sharpe ratios mighty. Keep questioning, keep quanting!📈
PS: What’s your typical holding period?
This is an invitation-only access to our QUANT COMMUNITY, so we verify numbers to avoid spammers and scammers. Feel free to join or decline at any time. Tap the WhatsApp icon below to join
Appendix
By the way! You can find my notes about all of this topics here. Enjoy it!