Table of contents:
Introduction.
Risk and limitaitons of online models.
Batch K-Means
Introducing the online paradigm.
Initialization and path dependency.
The curse of dimensionality and search optimization.
Evaluating performance on a moving target.
From clusters to signals.
Introduction
Alright team, let’s dive deeper into something we've all painfully experienced: You spend days meticulously crafting a K-Means clustering model—furthermore, you have decided to use it incorrectly to classify market regimes instead of applying it to other processes. The backtest results look flawless—you're confident and ready.
But then, the model goes live, and within weeks, your PnL starts bleeding heavily. So, what happened? Simply put, markets aren't static—or simply, that application to identify market regimes is nonsense. But ok, let's proceed with the same example: what was confidently classified as high volatility last quarter might now merely be background noise. That perfect momentum regime you painstakingly identified suddenly fractures into several distinct new states, and your static model has no clue how to adjust.
We've all seen it: those carefully crafted clusters that once captured clear market states now blur and shift unpredictably. Economic reports, central bank decisions, sudden geopolitical tensions, or even subtle changes in investor sentiment can swiftly redefine the landscape. Relying on static clusters is like trying to catch lightning in a bottle—it might look great initially, but inevitably, you end up chasing shadows.
Here's the crux of the issue: traditional batch clustering—the type that demands your entire historical dataset upfront—assumes a world frozen in time. Imagine navigating today's Manhattan with a detailed street map from the 1990s. The broad outlines and main avenues might still be correct, sure, but navigating the intricate, constantly evolving details—like new skyscrapers, blocked roads, and changing traffic flows—is nearly impossible. You'll end up lost, frustrated, and far from your destination.
In financial markets, this analogy couldn't be more accurate. New market participants, technological advancements, regulatory shifts, and evolving trading strategies constantly reshape the market terrain. Static models, anchored to historical datasets, rapidly lose their relevance, becoming not just inaccurate but potentially hazardous. They can mislead your strategies, resulting in positions that are poorly aligned with current market conditions, thus amplifying risks and eroding profits.
That’s exactly why Sequential Online K-Means isn't merely an incremental improvement—it's a fundamentally different, smarter way of thinking. Unlike batch methods, it doesn’t rely on outdated snapshots. Instead, Sequential Online K-Means is dynamic, learning and adapting continuously with each incoming data point. Think of it as a real-time heartbeat monitor, updating its understanding of market regimes tick by tick, trade by trade, and responding promptly to subtle shifts and significant shocks alike.
This approach doesn't just enhance performance; it aligns with the very nature of financial markets. As new trades occur, Sequential Online K-Means recalibrates its clusters, ensuring they accurately reflect the current market regime. It adapts quickly during periods of volatility, swiftly integrating new data to refine its regime classifications, thereby providing more reliable, timely, and actionable insights.
Let's be clear: we're not just refining an existing method; we’re addressing a fundamental misalignment between how batch algorithms view the market and how markets truly operate. This constant flux demands models that can flex and adjust with similar speed and sensitivity.
Risk and limitaitons of online models
Online models, including sequential k-means, offer the ability to learn from data streams in real time, but they come with a distinct set of risks and limitations that are crucial to understand.
Since online models learn sequentially, a model trained on past data may become inaccurate as the underlying data distribution shifts. This can happen suddenly (e.g., due to a market crash) or gradually (e.g., changes in customer behavior).
Errors in online learning can compound. If the model makes a mistake, that incorrect learning can influence future updates, potentially leading the model to drift further from an accurate state. Unlike batch models that can correct themselves with a global view of the data during retraining, online models have a more localized and sequential perspective.
While online models don't need to hold all historical data in memory, they must be fast enough to process incoming data points without falling behind. This can be a challenge in high-throughput environments, and the computational resources required can be a limiting factor.
Assessing the performance of an online model is more complex than for a batch model. There is no fixed test set. Evaluation must be done continuously on new, incoming data, making it difficult to get a stable measure of the model's accuracy. This requires robust monitoring and the ability to distinguish between model degradation and normal fluctuations in the data.
Batch K-Means
Let's get down to brass tacks. The problem with batch clustering, specifically K-Means, isn't a subtle philosophical point; it's a mathematical one. The algorithm's objective is to solve an optimization problem. Given a dataset X={x1,x2,...,xN}, we want to find a set of k centroids C={c1,c2,...,ck} that minimizes the inertia, or the within-cluster sum-of-squares.
Mathematically, we are trying to find:
Where Sj is the set of all data points xi assigned to cluster j, and cj is the centroid of that cluster—typically the mean of all points in Sj.
The standard algorithm to solve this—Lloyd's algorithm—is an iterative process:
Initialization: Pick k initial centroids.
Assignment step: Assign each data point xi to its nearest centroid.
Update step: Recalculate each centroid cj as the mean of all points assigned to it.
Repeat: Repeat steps 2 and 3 until the assignments no longer change.
Notice the implicit assumption here. The entire dataset X must exist and be held in memory for this to work. The update step computes the mean across all points assigned to a cluster. This is the definition of a batch process. It presumes the world is a closed system, a finished book. In finance, we're lucky if we have the current page, and we know for a fact the next one is being written as we speak.
This leads to two critical failures in a financial context:
Covariate shift: It is the milder of the two. The distribution of our input features—covariates—changes, but the underlying relationship between inputs and outputs—the concept—remains the same. For example, the average daily trading volume might increase across the market, but the patterns that define a momentum regime might still hold. A batch model will struggle because its sense of scale is now off.
Concept drift: It is the true killer. The fundamental relationship we are trying to model changes. The very definition of a volatile market regime might change. What was considered high volatility in 2017 might be considered moderate in 2025. A model trained on the old concept is now fundamentally broken.
You can check more about batch clustering here:
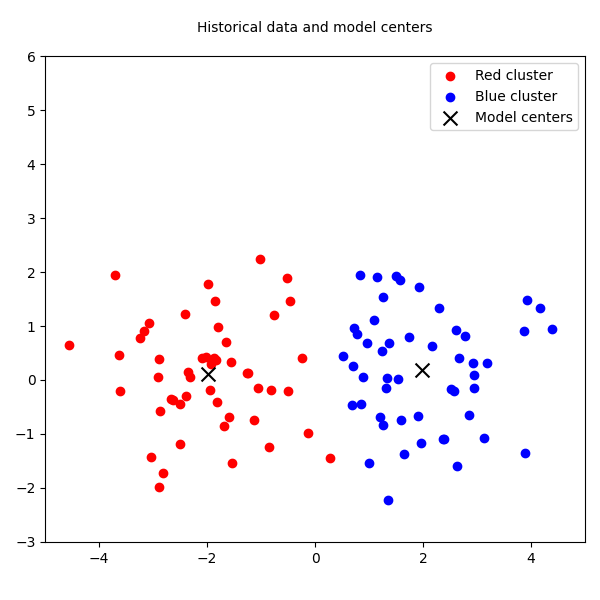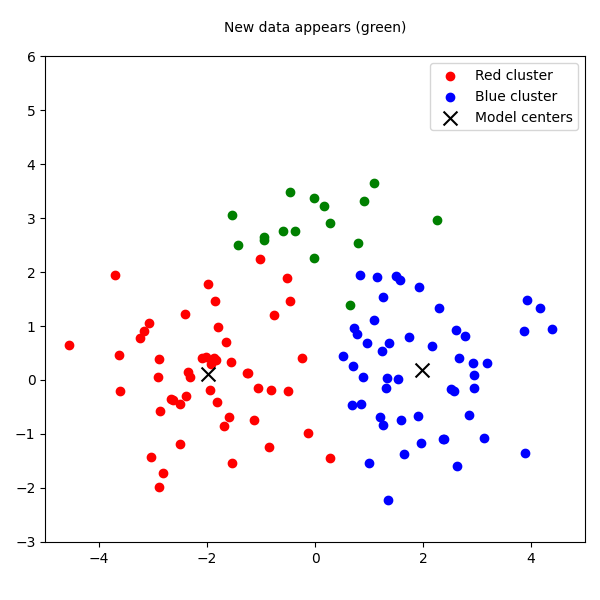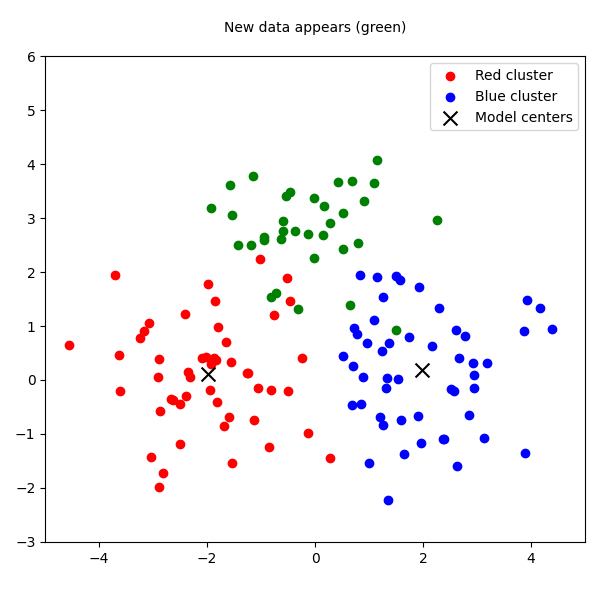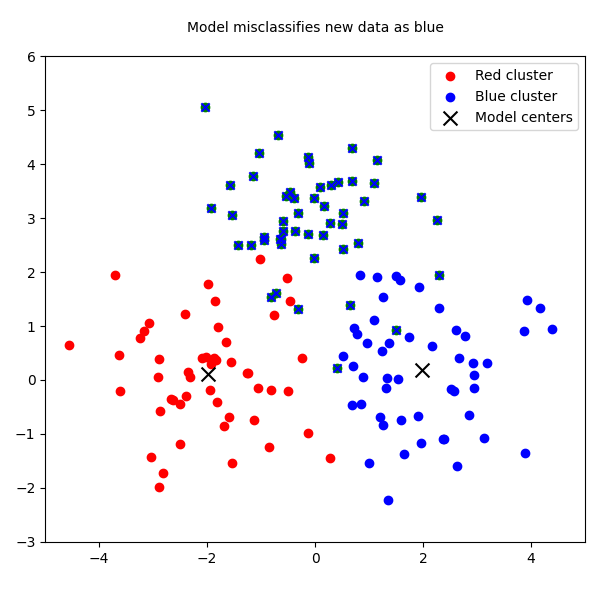
The batch model is blind. It has no mechanism to create a new cluster or even significantly adjust its existing ones. It simply shoehorns new reality into its old, rigid framework. This is the tyranny of the batch: forcing a dynamic process into a static representation.
To visualize this failure, we can use a simple plot. Imagine the red and blue clusters are our historical data. The batch model finds their centers—the black X's. Then, a new green cluster appears. The batch model has no choice but to misclassify all the green points as belonging to the blue cluster, because its structure is frozen.
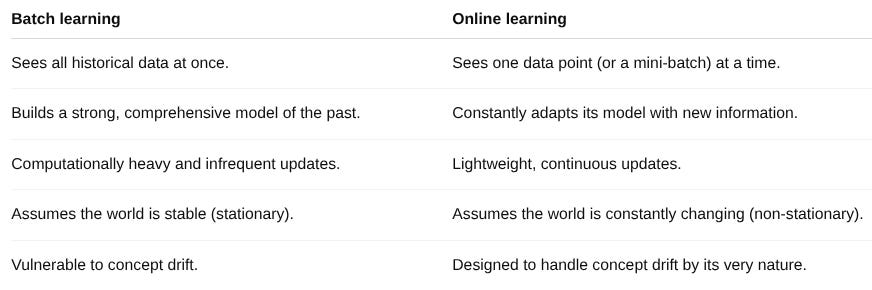
Introducing the online paradigm
If batch processing is a photograph, online learning is a live video feed. It processes the world frame by frame, or in our case, data point by data point.
The algorithm we're interested in, often called Sequential K-Means or Online K-Means, is a beautiful adaptation of the batch concept. It essentially performs a mini-update every time it sees a new piece of data.
Read more about online clustering here:
The core idea is to treat the centroid update as a form of Stochastic Gradient Descent. In batch K-Means, the update step moves the centroid to the exact mean of its assigned points. In online K-Means, we nudge the centroid towards the new data point that was just assigned to it.
Let's formalize this. Suppose at time t, we have a set of centroids. A new data point, xt+1, arrives from the market data stream. The process is as follows:
Assignment step: Find the winning centroid that is closest to xt+1.
\(j \;=\; \arg\min_{i \in \{1,\dots,k\}} \bigl\lVert x_{t+1} - c_i^{(t)}\bigr\rVert^2.\)Update step: Update only the winning centroid, cj.
\(c_j^{(t+1)} \;=\; c_j^{(t)} \;+\; \eta_{t}\,\bigl(x_{t+1} - c_j^{(t)}\bigr).\)All other centroids remain unchanged:
\(c_i^{(t+1)} \;=\; c_i^{(t)} \quad \text{for } i \neq j.\)
The magic is in the term ηt, the learning rate. What should it be? A simple and powerful choice is to make it inversely proportional to the number of points that have been assigned to that cluster so far. Let Nj(t+1) be the new count of points assigned to cluster j—including the latest one. Then we set ηt=1/Nj(t+1).
Let's unpack this update rule. It's an incremental update of the mean. The old centroid was the mean of Nj(t) points:
The new centroid should be the mean of Nj(t+1)=Nj(t)+1 points.
Substituting Nj(t)cj(t) for the sum:
Beautiful! Now, a little bit of algebra...
This is exactly our update rule with ηt=1/Nj(t+1). This learning rate has an interesting property:
It decreases over time for each cluster. When a cluster is young, new points have a large impact, causing the centroid to move quickly. As a cluster matures and accumulates thousands of points, a single new point has a very small impact, providing stability.
An animated plot is the only way to do this justice, showing the centroids as wandering points, pulled and pushed by the stream of incoming data, eventually settling into stable but not static configurations. Visualize an example with 3 clusters and 450 streams. Notice how the X's are updated chasing the center point of the cluster
Let's look at the implementation of this core logic in the OnlineKMeans class provided. The partial_fit method is where the action is—I'm using a simplified version for these snippets here but you'll find the entire script at the end of the article.