Data: Type of returns
Find out if log returns hold the key to overcoming market fear and decide which method will enhance your strategy in uncertain times
Table of contents:
Introduction.
Periodic returns.
Log returns.
When logs lie.
Tech bubbles & financial crashes
Which hero wins?
Introduction
Every great journey starts with a simple idea. Think of it like baking cookies: you have different recipes for the same delicious treat. In finance, we have two primary recipes to measure gains and losses—the periodic returns and the log returns. Although both methods lead to a final cookie—or total return—the way they mix the ingredients is quite different:
Periodic returns: It’s like adding chocolate chips one by one into your cookie dough. Each chip is counted separately, and the final cookie has a chunky texture that is very tangible.
Log returns: Now think of taking all the chocolate chips, grinding them into a fine powder, and then mixing them evenly into the dough. The cookie comes out smooth and uniform.
While periodic returns calculate gains using simple multiplication and division, log returns use logarithms to transform the process into a series of additions. In many advanced models, addition is easier to work with than multiplication.
Periodic returns
Periodic returns are calculated using simple arithmetic. Let’s start with a basic example. Suppose your lemonade stand earns $5 today and $10 tomorrow. The periodic return R is computed by:
Plugging in the numbers:
This means you have a 100% return on your lemonade stand investment. Just like grandma’s old calculator, the periodic return tells you the exact percentage increase—nice and straightforward.
Total return over multiple days
When returns occur over multiple days, things get a bit more interesting. For example, if your lemonade stand gains 10% on Day 1 and 20% on Day 2, you might think the total gain is 30%. However, the math shows a different story:
Calculating further:
Thus, the overall return is 32% and not the naive sum of 30%. The secret here is that returns multiply over time. This multiplicative nature is fundamental in finance and is one of the reasons why periodic returns are so popular in day-to-day accounting.
You can implemented by using this snippet:
def get_periodic_returns(prices):
"""
Calculate periodic returns.
For each consecutive pair of prices, the periodic return is:
R_t = (P_t / P_(t-1)) - 1
This function returns an array of returns.
Parameters:
prices (list or np.array): Array of asset prices.
Returns:
np.array: Periodic returns.
"""
prices = np.array(prices)
# Compute periodic returns for each period.
returns = prices[1:] / prices[:-1] - 1
return returnsWhere the cumulative return over T periods is given by:
Log returns
Log returns offer an alternative approach by converting multiplicative processes into additive ones. This transformation simplifies many mathematical operations, especially in the realm of financial modeling. Let’s revisit our previous example using log returns.
For a given return R, the log return r is defined as:
Taking our two daily returns, we compute:
For a 10% return:
The total log return over the two days is simply:
To convert the total log return back to a periodic return:
We arrive at the same 32% gain as before, but notice how the process is now a neat addition rather than a multiplication—a significant advantage when dealing with large datasets or complex models.
Implement it by using:
def get_log_returns(prices):
"""
Calculate log returns.
For each consecutive pair of prices, the log return is:
r_t = ln(P_t / P_(t-1))
This function returns an array of log returns.
Parameters:
prices (list or np.array): Array of asset prices.
Returns:
np.array: Log returns.
"""
prices = np.array(prices)
# Compute log returns using the natural logarithm.
log_returns = np.log(prices[1:] / prices[:-1])
return log_returnsWhy use logarithms!? Let’s break down the benefits of using log returns with a couple of simple points:
Additivity: Log returns allow you to add up daily returns without worrying about the compounding effect of multiplication.
Symmetry in gains and losses: With periodic returns, a 10% gain followed by a 10% loss does not bring you back to your starting point. However, log returns offer a more symmetric view: the log of 1.1 plus the log of 0.9 tends to cancel out more neatly—even though minor residual differences can appear.
Having laid out the basic recipes for periodic and log returns, we now move on to exploring a more nuanced aspect of log returns: the approximation methods that help us handle them mathematically. Our next section will delve into the oops moments—when the magic of logarithms isn’t as perfect as it seems.
When designing trading algorithms, one must decide how to process returns data. Using log returns can simplify the optimization process in models that rely on linear algebra, differential equations, or stochastic calculus. For example, the cumulative log return over a period can be calculated as:
This additive property makes it easier to compute gradients and perform optimization.
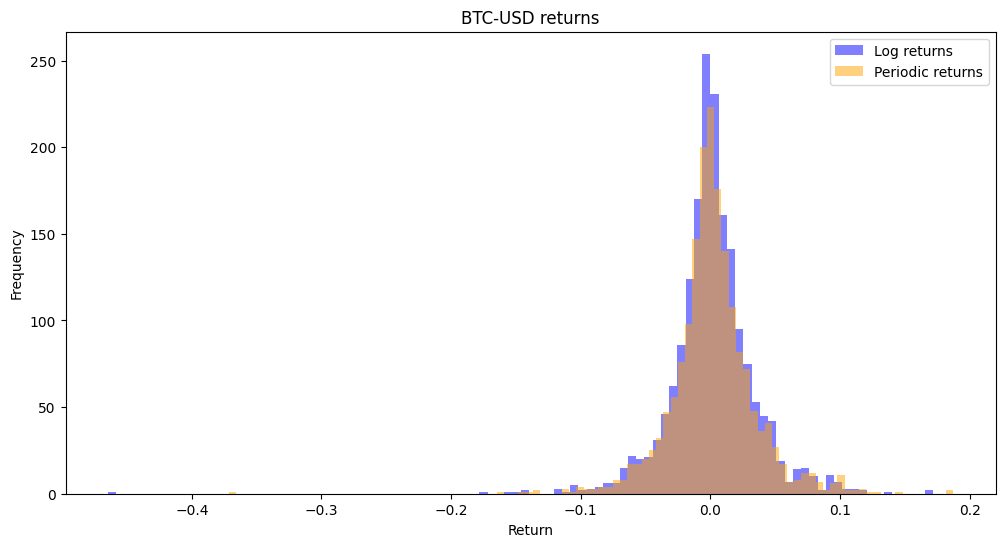
The next plot exposes the relationship between periodic and log returns:
When logs lie
While log returns are mathematically elegant, they are not without their quirks—especially when dealing with larger returns.
In mathematics, a common way to approximate functions is to use a Taylor series expansion. For the logarithm, the Taylor series of ln(1+x) is given by:
For small values of x (which represent small periodic returns), the series converges very quickly. In many practical situations, especially when |x| is tiny—like daily returns often are—, we can use a truncated version of this series:
This approximation is quite handy. However, as x grows larger, the neglected terms—like x3/3 and beyond—start to matter. These omitted terms are what we call the approximation error.
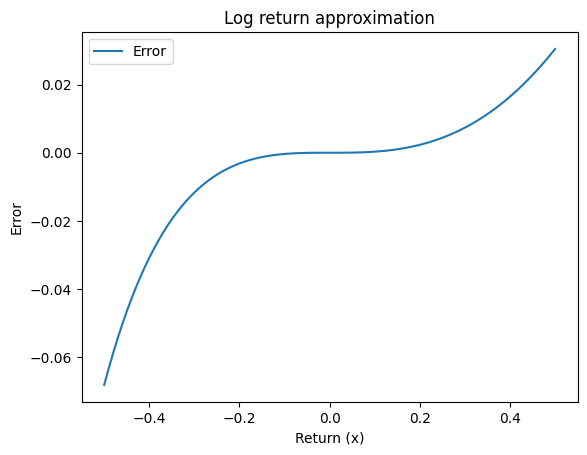
To understand the error better, let’s define the error function E(x) as the difference between:
When x is small, E(x) is nearly zero, but as x increases—or decreases into negative territory—E(x) can become significant. In algorithmic trading, even a small error can lead to misinterpretations of risk or return.
For example, the next plot shows that for |x| larger than about 0.2, the error begins to grow noticeably, with negative returns showing a larger deviation.
Now that we have dissected the approximation errors with log returns, it is time to see how these ideas play out in trading dramas.
Tech bubbles & financial crashes
Markets have a knack for drama—sometimes they soar like superheroes, and other times they plummet like a clumsy acrobat. These case studies will highlight the strengths and weaknesses of each approach.
The 2000 tech bubble:
During the tech bubble, stock prices in the technology sector experienced an exponential surge. Let’s model this! When a price grows exponentially over time, it can be expressed as:
Here, P0 is the initial price, k is the growth rate, and ttt is time. Taking the natural logarithm of both sides yields:
Notice how the logarithm converts an exponential growth pattern into a linear one—a straight line with slope k. This is one of the key benefits of log returns; they simplify the behavior of exponential growth.
Then, which one should I use to model the market?
Periodic returns: When using periodic returns during the tech bubble, the exponential growth can appear explosive. Investors might see returns like OMG, stocks are skyrocketing exponentially! This portrayal, while exciting, can be a bit misleading when trying to predict future behavior.
Log returns: Log returns, on the other hand, tame the exponential beast. By converting exponential growth into a linear trend, log returns allow us to analyze the data with a more balanced perspective. In this example, even as prices soared, the additive property of log returns provided a clearer picture of underlying growth.
The 2008 financial crisis:
The 2008 financial crisis was a period of significant market stress. During this time, the behavior of returns exhibited dramatic asymmetry.
Consider a market scenario where a 50% drop in asset price occurs:
To recover from that 50% drop, the asset must gain 100%—it needs to double in price just to get back to where it started:
This asymmetry is even more stark when looking at log returns. A 50% drop translates to:
which is about -69.3%. Notice that the magnitude is larger in absolute value than the -50% periodic return, highlighting how log returns can emphasize severe losses more than periodic returns. To regain the original price, the asset needs a +69.3%!!! Once again showing that log returns bring out the true severity of losses.
By comparing the tech bubble and the 2008 crisis, we see that both periodic and log returns offer valuable insights. Periodic returns provide a tangible, everyday measure of gains and losses, while log returns offer a refined lens that smooths out exponential growth and accentuates severe losses.
Besides systems that were designed during these turbulent times had to account for extreme movements in asset prices. Models built using log returns were better at capturing the risk of large drawdowns.