Models: Combining predictions
Harnessing the power of ensembling and formulaic alphas for robust predictive models
Introduction
The other day, several of you asked me for more details about a previous post—specifically about rule assembly. I’ve decided to expand on it and dive a little deeper into the topic. Let's start by illustrating this with a metaphor 😇
It's 6:00 p.m. and you're participating in a cooking competition where the challenge is to recreate a dish just by tasting it. You could trust one friend’s guess, but they might mistake cinnamon for paprika. Instead, if you gather input from a group—one who knows spices, another who bakes, and a third who just eats a lot—you can blend their insights and get much closer to the real recipe. This is the power of ensembling—combining multiple perspectives to refine decisions.
And what does all of this have to do with formulaic alpha or voting?
A formulaic alpha works the same way. It’s a rule-based approach that turns raw data into predictions. For example:
If the asset price drops by 1.5% and there is an increase in volume, then a reversal might occur.
If the asset price changes by 2% and there is a gap, then the price goes up.
Let’s create a silly-but-instructive alpha for predicting whether your cat will knock over a vase:
Input Data: Time since last meal (hours), number of laser pointer zooms in the past 10 minutes.
Rule: If
(time_since_meal > 2) AND (laser_zooms < 3), predict:
Does it really work?
Hungry cats (time since meal > 2) are grumpy.
Under-stimulated cats (few laser zooms) seek chaos.
Combine the two, and voilà—a predictive alpha!
Let’s assume:
A cat is hungry (time_since_meal > 2) 40% of the time → P(H) = 0.4
A cat is bored (laser_zooms < 3) 60% of the time → P(B) = 0.6
If hunger and boredom were independent, the probability of both occurring would be:
But our alpha claims 85%! That’s because we’re not merely calculating the raw probability of hunger and boredom coinciding. We’re estimating the probability of vase destruction given those conditions, a conditional probability:
where:
VVV = Vase destruction
HHH = Hunger
BBB = Boredom
Our model assumes that when both conditions are met, cats become tiny agents of entropy with 85% reliability. Not a certainty, but way better than random guessing.
But wait, watch out for this! When constructing an ensemble of formulaic alphas, adding multiple rules may seem like an intuitive way to improve predictive power. However, using more than two rules at once without a structured approach often leads to diminishing returns or even degradation of signal quality—you already know what I prefer: <2 rules—better for everybody.
The key reasons are:
Compounding noise instead of signal:
Each formulaic alpha is a mathematical rule designed to extract a predictive edge from market data. When you stack multiple rules without careful sequencing, you risk:
Introducing contradictory or redundant conditions.
Accumulating noise rather than refining the signal.
Overfitting to historical data rather than capturing a robust, repeatable pattern.
Interaction effects:
When two rules are combined, their interaction is somewhat manageable—either reinforcing or correcting each other. However, adding a third, fourth, or fifth rule increases the complexity exponentially, making it hard to:
Identify which component actually adds value.
Debug and optimize the system.
Maintain robustness across different market conditions.
The best approach is sequential filtering, where each additional rule should only enhance the strength of the previous one rather than introduce a completely new condition.
Here some examples:
Don't use any of them, they are completely useless, they are just for illustration.
The idea is that these structures guarantee:
Stepwise improvement: Each new rule acts as a refinement layer, filtering out false positives or optimizing execution conditions.
Preservation of edge: The original predictive power remains intact rather than being diluted by excessive constraints.
Better generalization: Instead of tailoring multiple conditions to fit past data, the sequence adapts dynamically.
But even applying a sequential filter, formulaic alphas can fail spectacularly. Why?
Overfitting yesterday’s news: If your alpha is too tuned to past data, it’ll fail in new scenarios.
The butterfly effect: Tiny input errors can wreck predictions.
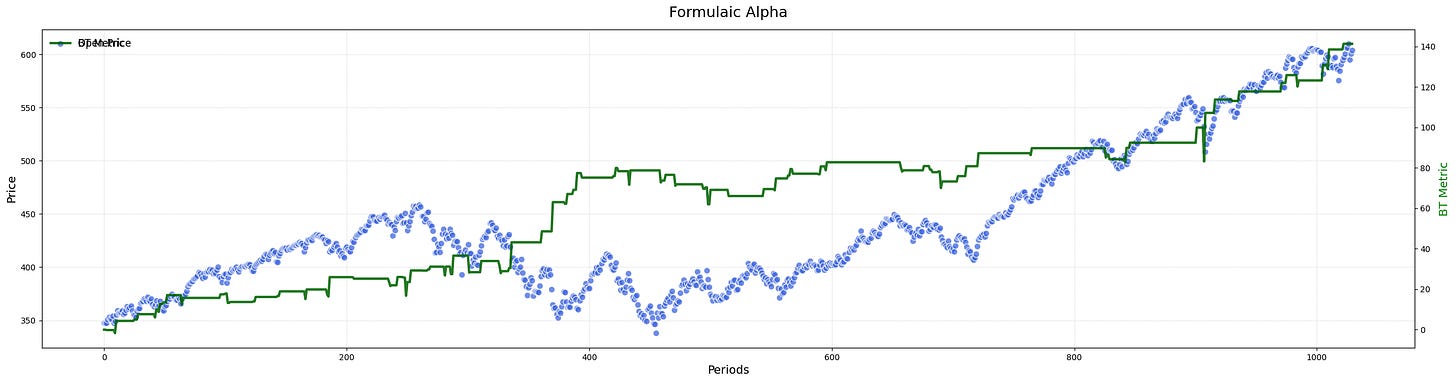
If you've done things right, you should get something like this:
Now that we’ve built our quirky alphas, it’s time to turn them into something quite interesting.
If you’re hosting a pizza party with five friends. Everyone argues about toppings:
Two scream: Pineapple belongs on pizza!—😮💨.
Three vote: Pepperoni forever!—classic.
You go with pepperoni—majority rules. This is ensemble voting in action! When alphas vote, we tally their predictions and pick the most popular one. Simple? Yes. Powerful? Not really.