Table of contents:
Introduction.
When smoothing data goes too smooth.
Why 1000 decision trees won't let you see the forest.
Feature engineering = Making up fairy tales
Introduction
It’s saturday and you’re at a birthday party. There’s a baby screaming, balloons popping, and your uncle belting out karaoke renditions of “Sweet Caroline.” To drown out the chaos, you put on your noise-canceling headphones and settle in to listen to Mozart. Suddenly, you miss the excitement—a piñata exploding overhead, a wild dance-off, and even a rogue Lego castle that sends your juice box flying.
In algorithmic trading, our market behaves like that screaming baby, full of chaotic noise and unpredictable events. In an effort to cancel out the “noise,” many traders apply sophisticated techniques such as denoising, Random Forests, and feature engineering. However, as we will show, these techniques can lead you astray, much like missing the best parts of the party.
When smoothing data goes too smooth
Let's start from the beginning: What’s denoising?
Donoising is a mathematical process aimed at extracting the underlying signal from a set of noisy observations.
Think of it as using a magic comb to tidy up your dog’s fur. The idea is that by removing the chaotic noise—i.e., the random fluctuations in stock prices—you can reveal a clear pattern that might help forecast future movements.
If we assume that a stock price P(t) can be decomposed as:
Where:
S(t) is the underlying signal, which may contain slow-moving trends and recurrent cycles.
ϵ(t) is the noise, representing short-term volatility and random shocks.
The challenge lies in the fact that, unlike in controlled environments, the distinction between S(t) and ϵ(t) is inherently blurry. An extreme event that appears to be noise might actually be the harbinger of a new trend. Thus, if you employ a denoising technique with a threshold parameter λ:
where D is your denoising operator, you risk filtering out crucial noisy data that contains the seeds of profitable opportunities.
In other words, by setting λ too high, you’re effectively saying, I only want the smooth, boring part of the market, and missing out on the wild swings that sometimes make—or break—a trading strategy.
In many classical approaches, one might employ tools like the Fourier transform or wavelet shrinkage to smooth out this noise. However, when you smooth too much, you risk removing not only the unwanted disturbances but also the important features that indicate profitable trading opportunities.
Imagine a barber who, in trying to give you a neat haircut, accidentally shaves off all your hair! The resulting bald Chihuahua isn’t exactly what you were hoping for. Moreover, these tools are only for labeling. Using them as a sign? It's suicide...
Here one of the classics, the Savitzky-Golay filter from the SciPy library:
import numpy as np
from scipy.signal import savgol_filter
import matplotlib.pyplot as plt
# Generate a fake stock price with a secret signal (sine wave)
t = np.linspace(0, 10, 100)
signal = np.sin(t) * 10 # The "real" pattern
noise = np.random.normal(0, 5, 100) # Chaos (aka market reality)
price = signal + noise
# Denoise it!
denoised = savgol_filter(price, window_length=50, polyorder=2)
# Plotting to visualize the effect
plt.figure(figsize=(10, 5))
plt.plot(t, price, label="Original price (noisy)")
plt.plot(t, denoised, label="Denoised price", linewidth=3)
plt.legend()
plt.title("Missing the turning points")
plt.xlabel("Time")
plt.ylabel("Price")
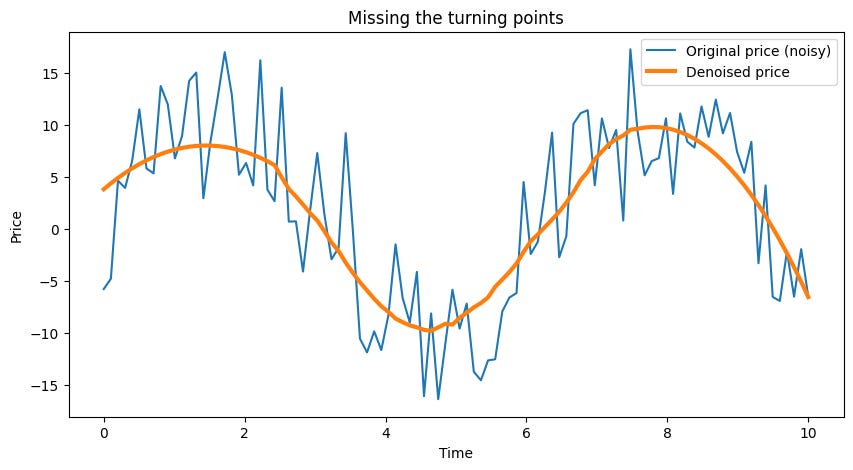
plt.show()In this experiment, the denoised curve looks smooth—almost too smooth. It fails to capture the rapid fluctuations—the turning points—in the actual price, leading to delayed responses in trading decisions.
Essentially, you’re buying late and selling late, and before you know it, your allowance—or trading capital—is evaporating.
But all is not lost, if you are interested take a look at this other version. It is more robust and better than the original filter. All the bugs that Scipy has have been removed. Take a look at my other article:
A more sophisticated approach to denoising employs wavelet transforms. The idea is to decompose the signal into wavelet coefficients and then apply a thresholding operation:
Here:
wk are the wavelet coefficients, representing the strength of the signal at different scales.
ψk are the wavelet functions.
Threshold(wk) sets to zero all coefficients below a certain level.
In markets, rare and extreme events—think of the GameStop saga—manifest as large coefficients. If we threshold these out, we lose the “surprise” factors that often lead to dramatic price movements. It’s like editing out all the explosions from an action movie: you end up with a film about cars discussing tire pressure.
Thus, the very process designed to clarify the picture inadvertently erases critical information, leaving you with a sanitized version of the market that fails to alert you to profitable—or dangerous—anomalies.